Statistiques
Page 1 sur 1
 Statistiques
Statistiques
Un fil pour recenser des liens, des ressources et des trucs qui peuvent intriguer quand on débute ou oublie cette branche particulière et pas forcément très intuitive.
Et éventuellement s'ouvrir l'esprit voire éviter de dire des grosses âneries
Et éventuellement s'ouvrir l'esprit voire éviter de dire des grosses âneries
stv82- Messages : 501
Date d'inscription : 28/01/2015
Localisation : Alpes du Nord
 Re: Statistiques
Re: Statistiques
EDIT 20180313: Ajout distributions binomiale/normale/poisson + théorème central limite
Rédaction en cours
A vérifier:
- niveau de confiance versus intervalle de confiance ? c'est bien lié ? exemple: niveau 95% -> une p=12% donne une p "vraie" 12 -1.96*... < p < 12 + 1.96*...
http://dimension.usherbrooke.ca/dimension/ssrerreurs.html
http://www.astro.ulg.ac.be/cours/magain/STAT/Stat_Main_Fr/Chapitre5.html
http://www.unipsed.net/ressource/c2-statistiques-descriptives/
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_central_limite
https://fr.surveymonkey.com/mp/sample-size/
http://icp.ge.ch/sem/cms-spip/spip.php?article1641
http://www.chups.jussieu.fr/polys/biostats/poly/POLY.Chp.10.3.html
https://seniorsecondary.tki.org.nz/Mathematics-and-statistics/Glossary/Glossary-page-S
calculateurs
http://www.rmpd.ca/calculators.php
http://www.init-marketing.fr/test-fiabilite-resultats/
des endroits où je rappelle avoir rencontré des stats à l'école (pour chercher des cours éventuellement)
- en terminale (il me semble mais plus très sûr)
- école d'ingé (stats plutôt avancées, avec tests de khi-deux et compagnie)
- cours de psychométrie en 2ème année de FAC de psycho (les cours sont alors souvent très détaillés car c'est un peu la bête noire de ces étudiants !)
Il y a plein d'occasions de mesurer tout un tas de choses et d'essayer d'en faire une synthèse ou un résumé.
On aurait très bien pu penser que la plupart des choses que l'on peut mesurer se serait distribuée harmonieusement de manière "plate".
Par exemple, si on mesurait des individus en disant que la hauteur mesurée au cm près ne pouvait être que dans l'intervalle 150cm → 200cm, il y aurait alors
- 2% de gens qui feraient 151cm
- 2% de gens qui feraient 152cm
- 2% de gens qui feraient 152cm
...
- 2% de gens qui feraient 200cm

Mais en réalité, les gens très grands détonnent dans le paysage par exemple, parce qu'ils sont peu nombreux. Ce n'est donc pas plat.
On voit plutôt quelque chose comme cela :
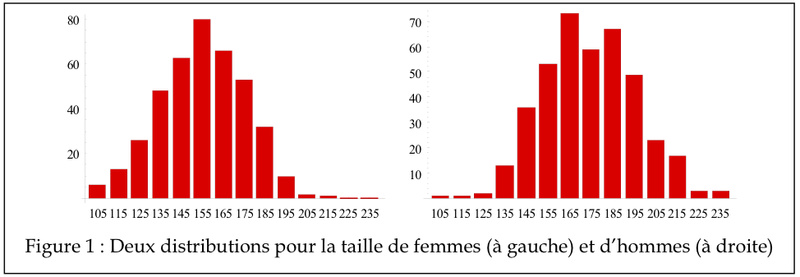
Il se trouve qu'apparemment beaucoup de choses que l'on peut mesurer de manière continue dans la nature se concentre fortement autour de la moyenne de ce qu'on mesure, et que plus on s'écarte de la moyenne moins on a de chances de trouver de quoi réaliser une mesure.
Je crois qu'on dit que les données suivent une loi normale.
Il me semble que c'est Laplace qui s'est déchaîné avec son théorème central limite qui permet de déduire une loi des erreurs.
De mémoire, ça dit entre autres choses que plus l'échantillon est grand, plus les données seront conformes à la distribution normale.
Ça marche pour la taille d'un individu, son tour de tête, son QI, son rapport taille index/annulaire, etc.
Dans la pratique, ce sont bien souvent des grandeurs discrètes (par exemple, arrondies au cm dans le cas de la taille car même si on mesure une grandeur continue on est bien souvent obligé d'arrondir les mesures d'une manière ou d'autre) voire bornées (avec un couple min/max imposé par la mesure) mais qui peuvent prendre n'importe quelle valeur par ailleurs.
Quand on représente la fonction de densité "idéale" pour cette loi, par exemple celle de la loi normale centrée réduite, la fameuse courbe de Gauss, on voit qu'il y a une densité forte au centre, et plus on s'éloigne sur les côtés, plus la densité chute.

On voit plus haut que le graphique de la taille des femmes ressemblent vraiment beaucoup à cette courbe.
Parfois, il y a une transformation pour passer de la représentation brute à la courbe de Gauss.
Mais quel est l'intérêt ? Je ne sais plus trop. Mais imaginons que j'ai bien compris le but.
Cela peut permettre de parler en terme de moyenne, d'écart-type, de qui est où et en quelle proportion.
Dans sa forme plus utile, cela permet d'identifier des zones distinctes de fonctionnement, et de les adresser en tenant compte de telle ou telle spécificité. Par exemple, proposer un dépistage de l'hormone de croissance si on grandit trop vite/trop fort.
Dans sa forme délétère pour l'esprit pour moi, je serai tenté de dire qu'on peut vite tomber dans l'habitude de "ranger dans des cases", de cliver ci/ça, homme/femme, etc. qui peut amener un sentiment identitaire, genre... tiens se pignoler le jonc pour savoir si on est "normal", HQI, THQI par exemple
Mettons donc de côté ces aspects, et voyons plutôt ce qui est possible.
Dans la vue de Gauss, on raisonne en terme d'écart-type par rapport à la moyenne qui est en 0.
Sur l'axe des abscisses, on a le nombre d'écarts-types par rapport à la moyenne. Ça m'a toujours perturbé cet écart-type
Autant, j'étais capable d'appliquer la formule bêtement mais je n'ai jamais vraiment compris sa signification tangible.
Encore aujourd'hui, à chaque fois que je tombe dessus au détour d'une lecture, je fais le lien avec la courbe de Gauss et je me dis "OK, donc si on s'écarte de cette valeur autour de la moyenne, il y a 68% des mesures concernées".
Bon, en tout cas, si on intègre la proportion entre -1 et 1, on a 68% de l'espace sous la courbe qui sera colorié.
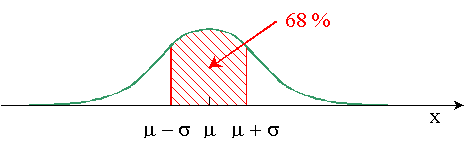
Si on reprend l'exemple avec la taille des femmes, on pourrait supposer à vue d’œil une moyenne à 155cm et un écart-type de 10cm environ. Donc, si cela suivait une loi binomiale "parfaite", 68% des femmes se trouveraient entre 155-10 = 145cm et 155+10 = 165cm
Ensuite, si on s'écarte de deux écarts-types, trois écarts-types, on va avoir de plus en plus de mesures concernées, et de moins en moins si on est dans les deux branches extrêmes.

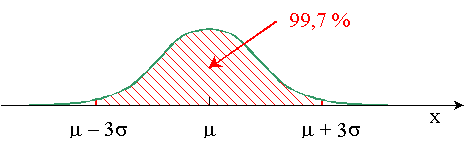
D'accord, c'est bien gentil ces graphiques mais quel est le but au final ?
Je dirais bien qu'en tant qu'humain, on est tous sujets à faire des statistiques. Et moi le premier à ce moment-là ("on est tous") !
Bon de manière plus nuancée, on a habituellement tendance à recouper des informations, en faire des moyennes de manière plus ou moins intuitive et s'accrocher à ces conjonctures ensuite.
Si on peut critiquer le caractère intuitif de celles que l'on fait à notre niveau sans réfléchir, il y a un corollaire vachement utilisé au fait que la majorité des choses que l'on mesure suive une loi normale.
Et là pour le coup, ça repose sur une réalité mathématique : si un phénomène suit une loi normale, il n'est pas nécessaire d'avoir 100% des données pour reconstituer la totalité des mesures possibles.
Cela signifie que prendre un sous-échantillon permet de généraliser les résultats ensuite. C'est utilisé dans plein de domaine (sondages d'opinion, publications scientifiques, etc.).
J'aime bien une des phrases de wikipédia :
Prenons un cas d'exemple extrême pour illustrer le cas où on est en erreur.
Un individu un peu miro se rend dans une conférence. Il ne voit que deux personnes : sur sa gauche et sa droite. Ce sont deux femmes.
Il en déduit que 100% des autres personnes de la salle sont des femmes.
Là une réaction possible va être "N'importe quoi, il ne peut pas déduire ça en regardant seulement deux personnes, ça ne veut rien dire"
Si, il peut mais avec niveau de confiance très faible, ou un intervalle de confiance très large. Et là, ça choque beaucoup.
Par contre, balancer que 95% des utilisatrices sont satisfaites dans une publicité pour une crème, avec un échantillon de x personnes marqué en petit en bas de l'image, ça choque moins !
Du coup, les publicitaires s'en donnent à cœur joie.
FIXME: trouver une image de pub d'exemple + calculer l'intervalle de confiance
Je cherchais une image d'une publicité sur le site de l'INA mais pas moyen de me rappeler
À défaut, voici un autre exemple avec une crème pour le visage :

Et le tableau en gros plan :

Là, le résultat n'est pas binaire (un utilisateur étant satisfait ou non par exemple). C'est un pourcentage de diminution des rides.
Un échantillon de 50 femmes a visiblement vu ses rides diminuer.
Partons du principe que c'est vrai, et que les chiffres n'ont pas été maquillés artificiellement par exemple, par le choix d'un un arrondi supérieur pour l'appareil qui mesure la profondeur des rides.
Le danger est alors la généralisation de ce sous-ensemble à la population entière.
Pourquoi ?
On peut tomber dans un cas où les choses mises en avant ne sont pas à l'origine du résultat annoncé. Dans le cas de cette crème, ça peut être que cet échantillon de femmes a mieux dormi, a changé son alimentation, a eu moins de fluctuations hormonales, était plus détendu, bref tout un tas de choses mais ayant une dépendance avec le jour du test ou la façon de mesurer. Je crois qu'on appelle ce genre de choses un biais statistique mais parfois je suis mal à l'aise avec la portée et les implications des biais. C'est difficile de se rendre compte.
Je crois qu'on dit l'échantillon n'est pas représentatif de la population mère.
Essayons de calculer l'intervalle de confiance pour la valeur de -18%.
Cette valeur signifie que sur ces 50 personnes, il y a eu une réduction de 18% en moyenne.
Mais peut-on généraliser à l'ensemble des femmes et surtout avec quelles marges d'erreur ?
FIXME: calculer
FIXME: retrouver le graphique dynamique où on voyait les anomalies se corriger au fur et à mesure que le nombre de participants augmentaient
Pour une publicité, tout le monde se fout qu'ils aient généraliser à partir de "rien".
Par contre, ça devient gênant quand des scientifiques publient des articles.
Pour être publié, il me semble qu'il faut un intervalle de confiance à 95%.
En d'autres termes, 5% de chances de se tromper.
FIXME: si la population mère ne suit pas tout-à-fait une loi normale
Quand on lit un article scientifique, à la lecture de telle ou telle donnée sur une population, on devrait plutôt lire "l'observation du petit sous-échantillon de la population, nous permet de généraliser cela à la population entière avec 95% de chance de dire vrai, si le phénomène respecte telle ou telle loi statistique".
https://fr.surveymonkey.com/mp/sample-size/

Personnellement, je me suis trimballé une confusion longtemps là-dessus.
Alors, si j'ai bien compris :
La distribution de poisson est une autre distribution de probabilités discrète utilisée pour décrire l'occurrence d'événements peu probables dans un grand nombre d'essais répétés, indépendants et limités dans le temps. Quand la probabilité est très faible et le nombre de répétitions élevé, elle se calque sur une distribution binomiale.


Voir http://zoonek2.free.fr/UNIX/48_R_2004/07.html pour plus de schémas
test du χ2 (khi-deux)
Rédaction en cours
A vérifier:
- niveau de confiance versus intervalle de confiance ? c'est bien lié ? exemple: niveau 95% -> une p=12% donne une p "vraie" 12 -1.96*... < p < 12 + 1.96*...
Liens
http://dimension.usherbrooke.ca/dimension/ssrerreurs.html
http://www.astro.ulg.ac.be/cours/magain/STAT/Stat_Main_Fr/Chapitre5.html
http://www.unipsed.net/ressource/c2-statistiques-descriptives/
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_central_limite
https://fr.surveymonkey.com/mp/sample-size/
http://icp.ge.ch/sem/cms-spip/spip.php?article1641
http://www.chups.jussieu.fr/polys/biostats/poly/POLY.Chp.10.3.html
https://seniorsecondary.tki.org.nz/Mathematics-and-statistics/Glossary/Glossary-page-S
calculateurs
http://www.rmpd.ca/calculators.php
http://www.init-marketing.fr/test-fiabilite-resultats/
des endroits où je rappelle avoir rencontré des stats à l'école (pour chercher des cours éventuellement)
- en terminale (il me semble mais plus très sûr)
- école d'ingé (stats plutôt avancées, avec tests de khi-deux et compagnie)
- cours de psychométrie en 2ème année de FAC de psycho (les cours sont alors souvent très détaillés car c'est un peu la bête noire de ces étudiants !)
Loi normale et courbe de Gauss
Il y a plein d'occasions de mesurer tout un tas de choses et d'essayer d'en faire une synthèse ou un résumé.
On aurait très bien pu penser que la plupart des choses que l'on peut mesurer se serait distribuée harmonieusement de manière "plate".
Par exemple, si on mesurait des individus en disant que la hauteur mesurée au cm près ne pouvait être que dans l'intervalle 150cm → 200cm, il y aurait alors
- 2% de gens qui feraient 151cm
- 2% de gens qui feraient 152cm
- 2% de gens qui feraient 152cm
...
- 2% de gens qui feraient 200cm

Mais en réalité, les gens très grands détonnent dans le paysage par exemple, parce qu'ils sont peu nombreux. Ce n'est donc pas plat.
On voit plutôt quelque chose comme cela :

Il se trouve qu'apparemment beaucoup de choses que l'on peut mesurer de manière continue dans la nature se concentre fortement autour de la moyenne de ce qu'on mesure, et que plus on s'écarte de la moyenne moins on a de chances de trouver de quoi réaliser une mesure.
Je crois qu'on dit que les données suivent une loi normale.
Il me semble que c'est Laplace qui s'est déchaîné avec son théorème central limite qui permet de déduire une loi des erreurs.
De mémoire, ça dit entre autres choses que plus l'échantillon est grand, plus les données seront conformes à la distribution normale.
https://fr.wikipedia.org/wiki/Loi_normale a écrit:La loi normale est l'une des lois de probabilité les plus adaptées pour modéliser des phénomènes naturels issus de plusieurs événements aléatoires.
Ça marche pour la taille d'un individu, son tour de tête, son QI, son rapport taille index/annulaire, etc.
Dans la pratique, ce sont bien souvent des grandeurs discrètes (par exemple, arrondies au cm dans le cas de la taille car même si on mesure une grandeur continue on est bien souvent obligé d'arrondir les mesures d'une manière ou d'autre) voire bornées (avec un couple min/max imposé par la mesure) mais qui peuvent prendre n'importe quelle valeur par ailleurs.
Quand on représente la fonction de densité "idéale" pour cette loi, par exemple celle de la loi normale centrée réduite, la fameuse courbe de Gauss, on voit qu'il y a une densité forte au centre, et plus on s'éloigne sur les côtés, plus la densité chute.

On voit plus haut que le graphique de la taille des femmes ressemblent vraiment beaucoup à cette courbe.
Parfois, il y a une transformation pour passer de la représentation brute à la courbe de Gauss.
Mais quel est l'intérêt ? Je ne sais plus trop. Mais imaginons que j'ai bien compris le but.
Cela peut permettre de parler en terme de moyenne, d'écart-type, de qui est où et en quelle proportion.
Dans sa forme plus utile, cela permet d'identifier des zones distinctes de fonctionnement, et de les adresser en tenant compte de telle ou telle spécificité. Par exemple, proposer un dépistage de l'hormone de croissance si on grandit trop vite/trop fort.
Dans sa forme délétère pour l'esprit pour moi, je serai tenté de dire qu'on peut vite tomber dans l'habitude de "ranger dans des cases", de cliver ci/ça, homme/femme, etc. qui peut amener un sentiment identitaire, genre... tiens se pignoler le jonc pour savoir si on est "normal", HQI, THQI par exemple
Mettons donc de côté ces aspects, et voyons plutôt ce qui est possible.
Dans la vue de Gauss, on raisonne en terme d'écart-type par rapport à la moyenne qui est en 0.
Sur l'axe des abscisses, on a le nombre d'écarts-types par rapport à la moyenne. Ça m'a toujours perturbé cet écart-type
Autant, j'étais capable d'appliquer la formule bêtement mais je n'ai jamais vraiment compris sa signification tangible.
Encore aujourd'hui, à chaque fois que je tombe dessus au détour d'une lecture, je fais le lien avec la courbe de Gauss et je me dis "OK, donc si on s'écarte de cette valeur autour de la moyenne, il y a 68% des mesures concernées".
Bon, en tout cas, si on intègre la proportion entre -1 et 1, on a 68% de l'espace sous la courbe qui sera colorié.

Si on reprend l'exemple avec la taille des femmes, on pourrait supposer à vue d’œil une moyenne à 155cm et un écart-type de 10cm environ. Donc, si cela suivait une loi binomiale "parfaite", 68% des femmes se trouveraient entre 155-10 = 145cm et 155+10 = 165cm
Ensuite, si on s'écarte de deux écarts-types, trois écarts-types, on va avoir de plus en plus de mesures concernées, et de moins en moins si on est dans les deux branches extrêmes.


Erreur d’échantillonnage et intervalle de confiance
D'accord, c'est bien gentil ces graphiques mais quel est le but au final ?
Je dirais bien qu'en tant qu'humain, on est tous sujets à faire des statistiques. Et moi le premier à ce moment-là ("on est tous") !
Bon de manière plus nuancée, on a habituellement tendance à recouper des informations, en faire des moyennes de manière plus ou moins intuitive et s'accrocher à ces conjonctures ensuite.
Si on peut critiquer le caractère intuitif de celles que l'on fait à notre niveau sans réfléchir, il y a un corollaire vachement utilisé au fait que la majorité des choses que l'on mesure suive une loi normale.
Et là pour le coup, ça repose sur une réalité mathématique : si un phénomène suit une loi normale, il n'est pas nécessaire d'avoir 100% des données pour reconstituer la totalité des mesures possibles.
Cela signifie que prendre un sous-échantillon permet de généraliser les résultats ensuite. C'est utilisé dans plein de domaine (sondages d'opinion, publications scientifiques, etc.).
J'aime bien une des phrases de wikipédia :
https://fr.wikipedia.org/wiki/Intervalle_de_confiance#Sondage_d'opinion a écrit:On cherche à estimer le pourcentage de personnes ayant une voiture rouge. Pour cela on effectue un sondage. Comme on ne sonde pas toute la population on a de bonnes chances de ne pas tomber exactement sur la bonne valeur mais de faire une erreur. On veut alors donner un intervalle qui a 95 % de chances de contenir la vraie valeur.
Prenons un cas d'exemple extrême pour illustrer le cas où on est en erreur.
Un individu un peu miro se rend dans une conférence. Il ne voit que deux personnes : sur sa gauche et sa droite. Ce sont deux femmes.
Il en déduit que 100% des autres personnes de la salle sont des femmes.
Là une réaction possible va être "N'importe quoi, il ne peut pas déduire ça en regardant seulement deux personnes, ça ne veut rien dire"
Si, il peut mais avec niveau de confiance très faible, ou un intervalle de confiance très large. Et là, ça choque beaucoup.
Par contre, balancer que 95% des utilisatrices sont satisfaites dans une publicité pour une crème, avec un échantillon de x personnes marqué en petit en bas de l'image, ça choque moins !
Du coup, les publicitaires s'en donnent à cœur joie.
FIXME: trouver une image de pub d'exemple + calculer l'intervalle de confiance
Je cherchais une image d'une publicité sur le site de l'INA mais pas moyen de me rappeler
À défaut, voici un autre exemple avec une crème pour le visage :

Et le tableau en gros plan :

Là, le résultat n'est pas binaire (un utilisateur étant satisfait ou non par exemple). C'est un pourcentage de diminution des rides.
Un échantillon de 50 femmes a visiblement vu ses rides diminuer.
Partons du principe que c'est vrai, et que les chiffres n'ont pas été maquillés artificiellement par exemple, par le choix d'un un arrondi supérieur pour l'appareil qui mesure la profondeur des rides.
Le danger est alors la généralisation de ce sous-ensemble à la population entière.
Pourquoi ?
On peut tomber dans un cas où les choses mises en avant ne sont pas à l'origine du résultat annoncé. Dans le cas de cette crème, ça peut être que cet échantillon de femmes a mieux dormi, a changé son alimentation, a eu moins de fluctuations hormonales, était plus détendu, bref tout un tas de choses mais ayant une dépendance avec le jour du test ou la façon de mesurer. Je crois qu'on appelle ce genre de choses un biais statistique mais parfois je suis mal à l'aise avec la portée et les implications des biais. C'est difficile de se rendre compte.
Je crois qu'on dit l'échantillon n'est pas représentatif de la population mère.
Essayons de calculer l'intervalle de confiance pour la valeur de -18%.
Cette valeur signifie que sur ces 50 personnes, il y a eu une réduction de 18% en moyenne.
Mais peut-on généraliser à l'ensemble des femmes et surtout avec quelles marges d'erreur ?
FIXME: calculer
FIXME: retrouver le graphique dynamique où on voyait les anomalies se corriger au fur et à mesure que le nombre de participants augmentaient
Pour une publicité, tout le monde se fout qu'ils aient généraliser à partir de "rien".
Par contre, ça devient gênant quand des scientifiques publient des articles.
Pour être publié, il me semble qu'il faut un intervalle de confiance à 95%.
En d'autres termes, 5% de chances de se tromper.
FIXME: si la population mère ne suit pas tout-à-fait une loi normale
Quand on lit un article scientifique, à la lecture de telle ou telle donnée sur une population, on devrait plutôt lire "l'observation du petit sous-échantillon de la population, nous permet de généraliser cela à la population entière avec 95% de chance de dire vrai, si le phénomène respecte telle ou telle loi statistique".
Exemple marge d'erreur et niveau de confiance
https://fr.surveymonkey.com/mp/sample-size/

Distribution binomiale versus distribution normale standard
Personnellement, je me suis trimballé une confusion longtemps là-dessus.
Alors, si j'ai bien compris :
- La distribution binomiale représente la probabilité de deux issues qui peuvent ou non se produire. Elle est discrète et donne une représentation avec des barres. Si on répète n fois une observation, chaque barre donne la probabilité qu'un certain nombre d'événements surviennent. Par exemple, si on lance 10 fois de suite une pièce de monnaie équilibrée, et qu'on regarde combien de fois on a eu le côté "pile" parmi ces dix lancers, on peut le représenter ainsi :
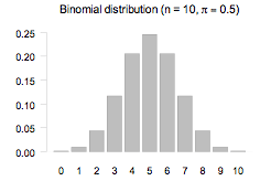
Si on refait plein de fois ces dix lancers, assez souvent on va voir sortir 3,4,5,6,7 piles. Mais il y a des cas très rares où 10 piles vont sortir. - La distribution dite normale est une distribution continue (au sens mathématique) liée à la distribution binomiale. En fait, quand n tend vers l'infini (n→∞), il y a un nombre infini de barre de largeur infinitésimale, et la loi binomiale devient alors la distribution normale :

Distribution de poisson
La distribution de poisson est une autre distribution de probabilités discrète utilisée pour décrire l'occurrence d'événements peu probables dans un grand nombre d'essais répétés, indépendants et limités dans le temps. Quand la probabilité est très faible et le nombre de répétitions élevé, elle se calque sur une distribution binomiale.


Voir http://zoonek2.free.fr/UNIX/48_R_2004/07.html pour plus de schémas
Indépendance entre deux variables aléatoires
test du χ2 (khi-deux)
Dernière édition par stv82 le Mar 13 Mar 2018 - 21:51, édité 11 fois
stv82- Messages : 501
Date d'inscription : 28/01/2015
Localisation : Alpes du Nord
 Re: Statistiques
Re: Statistiques
Merci pour ce post. Je crois qu'il est en effet essentiel de connaître un peu les statistiques. Elles devraient a minima toujours présenter le taille de l'échantillon par rapport à la population, que l'on puisse ainsi voir l'intervalle de confiance choisi.
Même si la représentativité mathématique a ses limites face à certaines réalités. Lorsque l'on fait des échantillonnages dans l'industrie par exemple.
Même si la représentativité mathématique a ses limites face à certaines réalités. Lorsque l'on fait des échantillonnages dans l'industrie par exemple.
Invité- Invité
 Re: Statistiques
Re: Statistiques
Pour ceux qui suivent, j'ai rajouté ce que je me rappelle sur les lois de distribution.
Bon sinon, je n'arrive plus à calculer les intervalles de confiance. Il me faudrait que je ressorte mes cours du grenier Tout ce que je trouve sur Internet me laisse croire que ça ne dépend que la taille de l'échantillon, mais pas de la taille de la population mère, alors que je me rappelais de l'inverse mais aussi bien j'ai mal pigé cette affaire ou les dessous de l'histoire avec le théorème central limite.
Tout ce que je trouve sur Internet me laisse croire que ça ne dépend que la taille de l'échantillon, mais pas de la taille de la population mère, alors que je me rappelais de l'inverse mais aussi bien j'ai mal pigé cette affaire ou les dessous de l'histoire avec le théorème central limite.
Bon sinon, je n'arrive plus à calculer les intervalles de confiance. Il me faudrait que je ressorte mes cours du grenier
stv82- Messages : 501
Date d'inscription : 28/01/2015
Localisation : Alpes du Nord
 Sujets similaires
Sujets similaires» Statistiques.
» RETOURS STATISTIQUES sur la participation au test ALIENS
» Cherche de l'aide pour comprendre les statistiques appliquées en psychologie
» Cherche de l'aide pour comprendre les statistiques appliquées en psychologie
» RETOURS STATISTIQUES sur la participation au test ALIENS
» Cherche de l'aide pour comprendre les statistiques appliquées en psychologie
» Cherche de l'aide pour comprendre les statistiques appliquées en psychologie
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
 Évènements
Évènements