John H. Conway

par paela Lun 13 Avr 2020 - 15:08

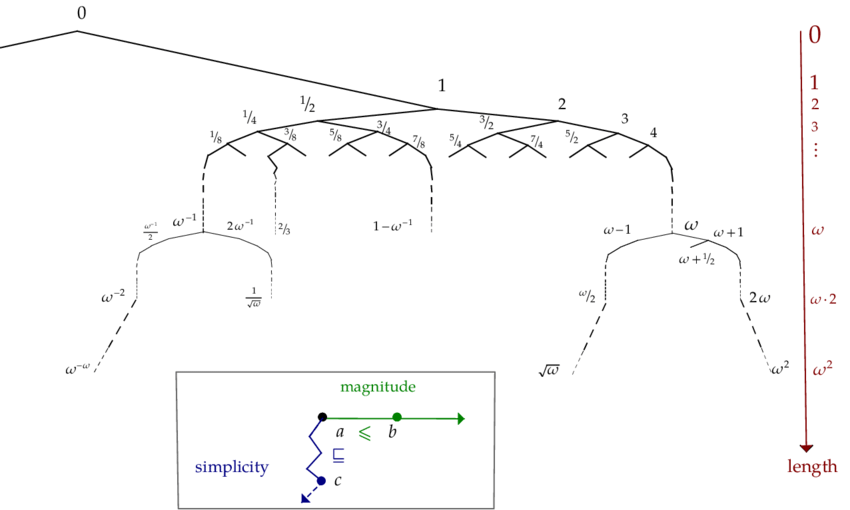
Le mathématicien anglais John Horton Conway est décédé le 11 avril 2020 après avoir contracté la covid-19. C'était un mathématicien prolifique avec une approche plutôt originale des mathématiques, axée sur le jeu et la simplicité. Il s'est intéressé à de nombreux problèmes, certains profondément ancrés dans l'histoire mathématique contemporaine, d'autres qui ont émergé grâce à sa grande créativité et à sa capacité d'émerveillement. Il a notamment découvert des tas d'objets mathématiques, géométriques ou de natures diverses dont une toute petite partie est représentée ici:

Précis de zoologie mathématiques:

Je vais faire dans ce topic une petite présentation de certains travaux qu'il a réalisés ou auxquels il a contribué. Ce sont seulement ceux que je connais au moins de loin. Je vous invite à compléter. Et bien sûr on peut discuter de ces choses librement aussi ici.

Je vais commencer par sa contribution à la classification des groupes finis simples. Ce n'est pas quelque chose qui tourne autour de Conway mais cela mérite quand même de figurer dans la liste. Ensuite je parlerai un peu des nombres surréels. Ensuite peut-être le jeu de la vie, mais je laisserais volontiers ça à d'autres.

par Topsy Turvy Lun 13 Avr 2020 - 15:17

C'est beau...
[J'ai trouvé.]

par Invité Lun 13 Avr 2020 - 15:47

Je crois que j'ai aussi trouvé Smile

par Topsy Turvy Lun 13 Avr 2020 - 15:57

I'm about to teach you how to do a nice little trick

I like this guy.

par I am So Sure Lun 13 Avr 2020 - 16:32

Le jeu et la simplicité...

study

Your latest trick. Dire straits. Musique...

par paela Lun 13 Avr 2020 - 21:47

Je vais faire dans ce topic une petite présentation [...]

Classification des groupes finis simples

Une contribution importante de Conway aux mathématiques est son travail concernant la classification des groupes finis simples (CDGFS).

Groupes finis simples
Un groupe fini est la donnée d'un ensemble fini G, dont je note les éléments a_0,...,a_n pour un certain nombre n positif ou nul, ainsi que d'une opération notée ici * qui à deux éléments a_i et a_j de G, éventuellement identiques, en associe un troisième noté a_i * a_j. Je dirai appliquer a_i à a_j pour désigner cette opération. A noter que j'aurais aussi pu dire appliquer a_j à a_i, car droite et gauche sont une affaire de convention.

On veut que cette opération respecte les règles suivantes où i, j et k sont des nombres quelconques entre 0 et n:
i) Qu'on ait toujours (a_i * a_j) * a_k = a_i * (a_j * a_k). Donc la priorité selon laquelle on effectue l'opération n'importe pas, ce qui fait que l'on peut retirer les parenthèses sans ambiguïté. Comme pour l'addition: (a+b)+c=a+(b+c) (essayez chez vous!), donc on écrit simplement a+b+c.
ii) Qu'on ait un élément, qu'ici je vais choisir comme a_0, tel qu'appliquer l'opération avec a_0 ne change rien, c'est-à-dire tel qu'on ait a_0 * a_i = a_i * a_0 = a_i. Cet élément est appelé le neutre pour l'opération; il n'en pense rien. Si * est l'addition de nombres, alors le neutre est 0.
iii) Qu'il existe toujours un élément a_i' tel qu'on ait a_i * a_i' = a_i' * a_i = a_0. C'est-à-dire qu'appliquer a_i à a_i' où l'inverse permet de revenir au neutre. L'élément a_i' est uniquement déterminé par a_i. On l'appelle l'inverse de a_i

Une intuition importante derrière ces objets est celle d'ensemble de transformations laissant invariante une forme géométrique. Prenez un objet chez vous, et choisissez des manipulations que vous pouvez lui faire, que vous pouvez ensuite faire dans le sens inverse pour revenir à la situation d'origine**. C'est le moment de sortir l'isocaèdre régulier du placard. Numérotez toutes ces transformations et leurs inverse a_0, a_1, etc... N'oubliez pas le neutre: ne rien faire**, et appelez-le a_0 je vous prie.
Regardez ce qu'il se passe lorsque vous en faîtes deux, a_j puis a_i, à la suite: cela vous donne une troisième transformation notée a_i * a_j. Elle est déjà dans la liste? Sinon ajoutez-là, et remarquez que pour faire l'inverse de a_i * a_j, il faut faire l'inverse a_i' de a_i, puis l'inverse a_j' de a_j, donc faire a_j' * a_i'. Ajouter tout ça à votre arsenal et continuez tant que la liste peut s'allonger.
Attention, la liste grossit assez rapidement si vous commencez avec beaucoup de choses. D'ailleurs, la vitesse de croissance de cette liste est tout un domaine d'étude en mathématiques qui est la théorie géométrique des groupes.
Si vous avez choisi au départ une transformation du genre le soulever d'un mètre, cela ne va jamais s'arrêter car il faudra aussi pouvoir le soulever de deux, trois, quatre mètres, etc... Si vous avez été prudent, à un moment la liste ne va plus s'allonger. Félicitations! Vous venez d'obtenir un groupe de transformations de votre objet. Si vous êtes parti d'un triangle il sera assez petit, si vous êtes parti d'une boule de pâte à modeler ou de votre chambre, il sera un peu balourd, mais l'entropie joue en votre faveur.
Cela fonctionne parce que le procédé général d'appliquer une transformation à la suite d'une autre respecte naturellement la première règle des opérations de groupe (notée i) plus haut).

A noter que contrairement à l'addition de nombres, votre opération aura peu de chance de se comporter de manière symétrique; au sens où faire a_j puis a_i ne sera pas la même chose que faire a_i puis a_j: en général a_i * a_j est distincte de a_j * a_i.

Ca c'est pour les groupes finis. Un groupe infini, c'est la même chose sans la contrainte que l'ensemble est fini. Un groupe fini est dit simple s'il ne peut pas être décomposé en un certain sens à l'aide de deux groupes plus petits. Une illustration: je prend un carré en papier et je le place dans un joli cadre carré parfaitement adapté aux dimensions. Je m'autorise deux opérations de base en plus du neutre a_0:
-le faire tourner d'un quart de tour dans le sens des aiguilles d'une montre: noté opération a_1
-le sortir du cadre, le retourner de droite à gauche (face du dessus au dessous donc) et l'y replacer sans avoir rien fait d'autre. Je note ça a_2. D'un point de vue mathématique, si on identifie les deux faces du papier, cela revient à faire une symétrie par rapport à l'axe vertical de symétrie.

Je vais utiliser un système de notation différent en parallèle: r (pour rotation) pour a_1 et s (pour symétrie) pour a_2. Si m est un nombre naturel et a_i est une transformation, alors je note aussi a_i^m l'application successive m fois de a_i à lui-même. La convention est a_i^0 = a_0 et que si n est négatif, alors a_i^n désigne l'inverse de a_i^(-n). Cette convention naturelle permet notamment d'avoir la propriété a_i^m * a_i^n =a_i^(m+n) dès lors que m et n sont des entiers relatifs.

Faisons notre liste initiale et appliquons la construction présentée plus haut. On a donc trois transformations de départ:
-Le neutre a_0.
-La rotation a_1 = r.
-La symétrie a_2 = s.
-Je note a_3 l'inverse de r, donc r^(-1). C'est la rotation d'un quart de tour dans l'autre sens. Puisque qu'il revient au même de faire quart de tour dans un sens ou trois quarts de tour dans l'autre, on a a_3 = r^3.
-L'inverse de a_0 est a_0 et l'inverse de s est s car faire deux fois la symétrie axiale revient à ne rien faire**.
Rajoutons maintenant les résultats d'application d'une transformation à une autre. On peut oublier ce qui fait intervenir le neutre a_0 puisqu'il n'a aucun effet.
-Je note a_4 la rotation d'un demi-tour dans le sens des aiguilles d'une montre. a_4 = r^2. Tiens, c'est aussi la rotation d'un demi-tour dans l'autre sens, soit a_4 = (r^(-1))^2=r^(-2). On voit que a_4 est son propre inverse, comme l'est s.
-Je note a_5 la symétrie axiale d'axe horizontal: prendre le carré et le retourner par devant soi. On a a_5 = a_4 * s = r^2 * s. L'inverse de a_5 est a_5 lui-même, comme pour s ou toute symétrie axiale.
-Je note a_6 la symétrie axiale d'axe oblique nord-ouest \ sud-est: prendre le carré avec la main droite par ces deux extrémités et retourner la main. On a a_6 = s * r. Cette transformation est aussi son propre inverse. Or l'inverse et obtenu en appliquant les inverses de s et r dans l'autre sens. Comme ce sont s et r^3 respectivement, on a: s * r = r^3 * s.
-Je note a_7 la symétrie axiale d'axe oblique nord-est / sud-ouest: prendre le carré avec la main gauche par ces deux extrémités et retourner la main. On a a_7 = s * r^3. De même que pour a_6, on a s * r^3 = r * s.
Ces transformations sont donc toutes de la forme r^k * s^p où k est un nombre entre 0 et 3 et p est un nombre entre 0 et 1.
On voit déjà que les inverses de ces transformations sont déjà dans la liste a_0,...,a_7. Par chance, il se trouve que les différentes applications a_i * a_j que l'on peut faire avec cette liste donnent des résultats qui sont déjà dedans, comme le montrent les tables suivantes:

Tables de groupes:

Donc ces huit transformations forment bien un groupe fini. Or si j'étais parti seulement de r ou de s, j'aurais obtenu des groupes plus petits R et S dont les éléments sont tous de la forme r^k et s^p respectivement (mêmes contraintes sur k et p). Ainsi, ce groupe, qui est appelé le groupe dihédral d'ordre hit, noté D_8, peut donc se décomposer à l'aide des deux groupes plus petits (et faciles à comprendre) R et S, respectivement à 4 et 2 éléments.

On peut aussi décomposer R davantage, car il contient (d'une manière particulière) le plus petit groupe formé des transformations a_0 et a_4.
Donc ni D_8 ni R ne sont simples, tandis que S l'est.

Un exemple de groupe fini simple de taille aussi grande que l'on veut est le suivant: on organise un concert avec un certain nombre n d'artistes musicaux (cette analogie date d'avant notre ère). On nous a donné la consigne de choisir dans quel ordre ils vont passer, sachant que chaque groupe passe une et une seule fois. Nos transformations sont les modifications du planning initial que l'on va prendre comme un planning quelconque fixé. Il peut s'agir d'inverser l'ordre dans lequel deux artistes passent, de faire passer le dernier en premier et donc de tout décaler d'un rang vers la fin, ou toute autre réorganisation imaginable. Ces trans formations sont appelées permutations de n. Je note P ce groupe. Ex si n=4 et les artistes sont Aaron, Björk, Céline Dion et David Bowie (j'ai dit que c'était avant notre ère), avec pour planning initial (A B C D). On a la permutation (A B C D) --> (C B A D) qui échange les premier et troisième artistes, et la permutation (A B C D) --> (D A B C) qui décale tout d'un rang vers la fin. Si on fait la première permutation, puis la seconde, alors on obtient la permutation (A B C D) --> (B A D C) qui n'est pas top d'un point de vue musical.
Les artistes se moquent un peu de savoir s'ils passent en premier, second, etc. Par contre, ils aiment bien savoir s'il passent après ou avant tel autre artiste, car cela joue beaucoup pour l'état du public. Cela fait qu'ils expriment un mécontentement à chaque occurrence dans le planning du fait que la permutation les fait passer après un artiste alors qu'ils devaient passer avant, ou l'inverse.
Puisque chaque mécontentement exprimé par A par rapport à sa situation vis-à-vis de B est lié à un mécontentement de B par rapport à sa situation vis-à-vis de A, il y a un nombre pair de mécontentements. Rapidement, on se rend compte que les transformations que l'on peut faire sont de deux types.
-celles, dites de type pair, qui génèrent un nombre de mécontentements qui est un multiple de 4, presque une chanson, qui plaît à entendre
-et les autres (chaos et désolation), dites de type impair.
On s'aperçoit aussi, avant de le démontrer, que si deux permutations a_i et a_j sont e type pair, alors leur inverse et a_i * a_j aussi. Ainsi l'ensemble des permutations de type pair est lui-même un groupe (deux fois) plus petit. En particulier, ce groupe noté A(n) et appelé groupe alterné (de taille n). Au fait P(n) est appelé groupe symétrique de taille n.
Il se trouve que sauf si n = 4, le groupe alterné A(n) est simple.

Classifier les groupes simples
Il y a une grande variété de groupes finis, et par définition tout groupe qui n'est pas simple peut se décomposer à l'aide de groupes qui eux sont simples. Les groupes finis simples sont donc des briques élémentaires de construction des groupes. D'où l'intérêt de les classifier.
il y a d'autres raisons pour lesquelles les groupes simples sont importants. Ils ont notamment un rôle à jouer dans l'étude des équations algébriques via la théorie de Galois, qui est à l'origine du développement de la notion de groupe.

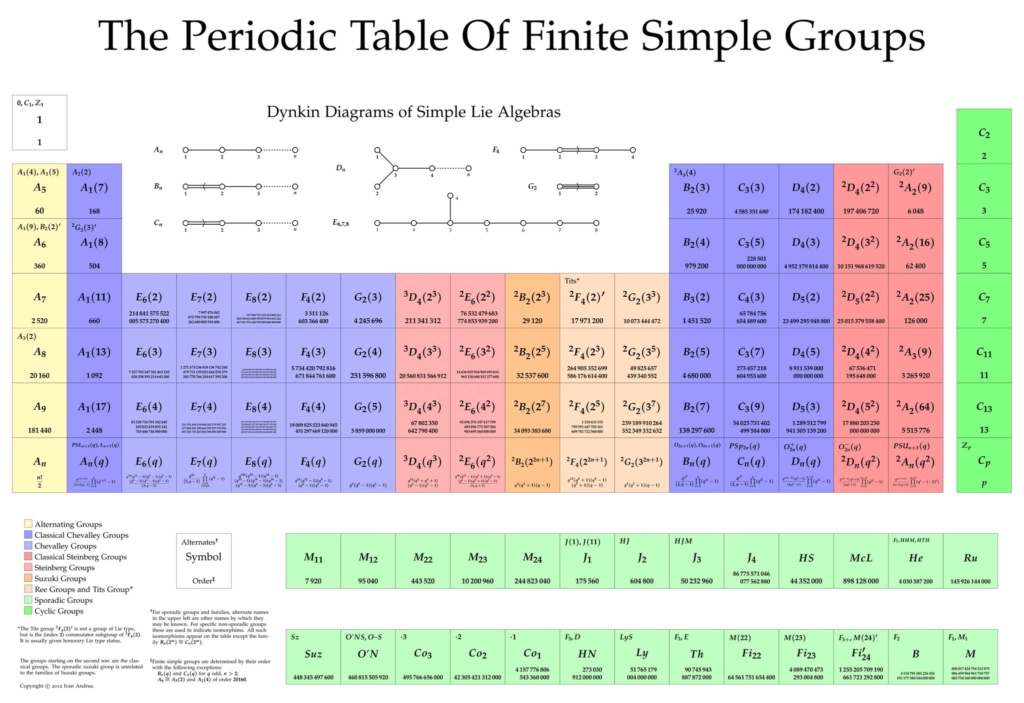
Table périodique des groupes finis simples:

La CDGFS est une grande aventure mathématique à laquelle ont participé de nombreux mathématiciens, soit dans la formulation progressive de la conjecture, soit dans la définition des classes de la classification, soit dans la recherche de groupes, soit dans la démonstration de l'appartenance à certaines catégories. Ainsi, Conway n'a eu comme tous les autres, qu'une petite part dans cette histoire. Mais la part de Conway est intéressante.

Que veut-on dire par classifier les groupes simples? Les ranger par classes, par famille si l'on veut, caractérisées par des propriétés communes. La classification n'est pas faîte selon un grand principe mathématique synthétique (du genre des types pair et impair des permutations), mais selon une organisation pratique qui a un sens tout aussi profond, au moins par endroits.
Il faut tout d'abord noter que si je n'ai présenté jusqu'ici que quelques groupes simples (les A(n) pour n distinct de 4, ainsi que S et R), c'est surtout par manque de temps. Depuis bien avant que la notion de groupe soit vraiment reconnue pour ce qu'elle est en mathématiques, divers domaines des maths ont produit leur lot de groupes finis simples.

Je commence tout de suite par spoiler la plus grande partie de la classification, qui ne concerne d'ailleurs pas Conway. Ce sont trois familles infinies de groupes simples finis "de la même provenance".

a) Le plus facile, ce sont les groupes comme S, qui ne contiennent qu'un élément a_1 et toutes les transformations a_i^k où k est un entier positif. Puisque a_1 satisfait a_1^p = a_0 pour un certain nombre p, le groupe est fini. Pour S c'est a_1=s et p=2. Si on veut que le groupe soit simple, il faut qu'on ne puisse pas diviser p par un entier plus petit (sauf 1), car si p = k m où 1<m<p, alors on a un plus petit groupe formé des a_1^q pour q <m grâce auquel on peut décomposer notre groupe. Donc il faut que p soit un nombre premier. Pour chaque nombre premier, on a un tel groupe dont la taille est ce nombre premier. Comme transformations, on peut imaginer des rotations d'un p-ième de tour autour d'un point du plan.

b) Ensuite, il y a les groupes alternés A(n). Attention, si n<4, alors ces groupes sont en fait dans la première catégorie, donc les nouveaux sont seulement ceux pour n>4.

c) Ensuite, il y a une autre famille trop compliquée à définir de groupes dits groupes de type de Lie. On peut très approximativement les décrire comme des sous-ensembles de groupes de transformations de certaines formes géométriques qui consistent en les éléments eux-même invariants par une certaine transformation. Bon, groupes de type de Lie. Malheureusement, les exemples intéressants ne sont pas facile à présenter. J'y réfléchirai.
Alors que les deux catégories précédentes sont "simples" à décrire, celle-ci est plus vaste et peut se découper en diverses catégories. Le gros de la conjecture se trouve dans l'établissement de la carte de cette catégorie et de sa frontière avec la catégorie des groupes sporadiques (voir plus loin).

d) Le groupe de (Jacques) Tits, qui est presque un groupe de type de Lie, mais pas vraiment, donc il est parfois classé avec, parfois avec les groupes sporadiques. Je le laisse là.

Groupes sporadiques
La dernière toute petite famille (finie) de groupes est celle des groupes sporadiques. Ces groupes sont des groupes finis simples, mystérieux, plantés là, qui n'appartiennent à aucune des familles mentionnées plus haut. Il y en a vingt-six! Vingt-six groupes qui ne correspondent à aucune des familles a), b) et c) ci-dessus. On peut bien sûr les regrouper selon d'autres critères, mais ils restent sporadiques à la fois dans leur nombre et leur mystère.
Pourquoi y a-t-il de grandes familles infinies, certaines variées certaines non, puis 27 groupes qui se baladent dans la nature? Je ne sais pas. Comment a-t-on pu être sûr que le dernier des groupes sporadiques était bien le dernier? Je ne sais pas non plus malheureusement et cela serait très probablement trop compliqué à expliquer (et pour moi à comprendre). Je peux donner des idées générales:
-L'établissement d'invariants élémentaires. Un invariant pour les groupes finis simples est quelque chose qui ne change pas lorsqu'on considère différentes présentations du même groupe. Dans l'idéal, on cherche des invariants facile à manipuler (en particulier des nombres entiers, ou des booléens: oui ou non). C'est encore mieux s'ils sont efficaces dans leur faculté à distinguer les groupes pour lesquels l'invariant n'est pas le même, et aussi pour rassembler les groupes pour lesquels il est le même.
L'invariant premier est le nombre d'éléments dans le groupe, appelé ordre du groupe. Le n de l'introduction. Il ne s'agit pas de lister les groupe par leur nombre d'éléments car cela donnerait une description chaotique. Ce qui est plus intéressant est de regarder des propriétés de ce nombre (des invariants si on veut!). Par exemple il est connu depuis le début du XXième siècle que si p et q sont premiers, alors un groupe qui possède p^k * q^l éléments n'est simple que s'il est dans la première famille de la classification (voir a)). Donc être simple et en dehors de la première famille implique déjà d'avoir trois diviseurs premiers pour le nombre d'éléments du groupe.
Ensuite, il y a des choses plus compliquées comme les groupes contenus dans ce groupe et qui ne sont contenu dans aucun groupe intermédiaire, et des outils plus fins comme la table des caractères.
-La représentation. Alors que les groupes sont des objets abstraits, donnée d'un ensemble et d'une opération, il est dans leur nature de se représenter comme des groupes de transformations de certaines choses, parfois géométriques, parfois plus combinatoires. Il y a des manières, mettons qu'un groupe satisfasse une certaines propriété faisant partie d'une bonne dichotomie, de le représenter comme un groupe de transformations. De cette manière, on range ce groupe dans telle ou telle catégorie. La théorie de la représentation des groupes finis est un puissant outil pour démontrer un tas de résultats non triviaux "facilement".
Une illustration fondamentale (mais assez triviale) est qu'on peut voir tout groupe fini G=a_0,...a_n comme un sous-ensemble du groupe de permutations P(n). Pour ce-faire, on imagine qu'au lieu d'organiser un festival de musique, on organise un festival du groupe G, où chaque élément va apparaître une et une seule fois. On s'autorise comme transformation seulement celles de la forme (a_0 a_1 ... a_n) --> (a_i * a_0 a_i * a_1 ... a_i * a_n) où a_i est un élément quelconque de G. Donc les permutations obtenues en appliquant le même a_i quelconque sur tous les a_i. Notons a_i° cette transformation. On peut voir qu'on a (a_i * a_j)° = a_i° * a_j°. Ainsi G est la même chose que le groupe de ces permutations particulières avec l'opération naturelle.
Donc si la classification était "les groupes qui sont des sous-ensembles d'un P(n)", alors on serait vite fixé.
Il existe des théorèmes de représentation qui sous certaines conditions montrent comment un groupe peut être vu comme un type particulier de groupes de type de Lie.

Pour mesurer à quel point ce que j'écris ici est une ultra-simplification, on peut méditer sur le fait que les preuves de correction de petites lacunes dans la classification ou de vérification qu'un groupe donné est bien sporadique font parfois plus des centaines de pages.

C'est le mathématicien William Burnside, a qui on doit la première démonstration du résultat sur les nombres premiers cités dans le paragraphe précédent, qui a trouvé la formulation "groupe sporadique". C'est ainsi qu'il qualifia cinq groupes finis simples étudiés par le mathématicien Mathieu, maintenant appelés les groupes de s Mathieu (M1, M2, M3, M4 et M5). Burnside a aussi formulé une onjecture plus forte que le précédent théorème: que tout groupe simple d'ordre impair fait partie de la première catégorie. Cela signifierait qu'on peut se concentrer sur les groupes d'ordre pair. La conjecture de Burnstein a été démontrée par Walter Feit et John G. Thompson. Elle porte maintenant le nom de théorème de Feit-Thompson. Leur preuve était d'une difficulté et d'une longueur hors norme pour l'époque, et certains pensent qu'elle marque un tournant dans la pratique de la recherche mathématique.
Les travaux de Thompson et Feit laissaient entrevoir la possibilité que des groupes finis simples de certains ordres donnés (175 560) existent. A cette époque, on pense encore que les cinq groupes de Mathieu sont, avec les nouvelles catégories de groupes de type de Lie qui sont découvertes, les dernières pierres dans la classification. Mais le mathématicien (bon tous les personnages de cette histoire sont des mathématiciens) Zvonimir Janko arrive à construire un groupe fini simple d'ordre 175 560, puis un autre plus gros, puis un troisième, d'ordre 50 232 960. D'autres mathématiciens prouvèrent l'existence de puis construisirent d'autres groupes sporadiques, jusqu'à ce qu'il y en ait onze au total.

Contribution de Conway
Conway a trente et un an lorsque le onzième groupe sporadique est découvert. Au Congrès international de mathématiques, tandis que Grothendieck ne vient pas chercher sa médaille Fields pour protester contre la guerre du Vietnam, Conway discute de mathématiques avec les gens présents. Sachant qu'il s'intéresse aux groupes finis simple, John McKay lui parle alors du réseau de Leech en lui suggérant que les transformations de ce réseau pourraient être intéressantes. Disons qu'un réseau est un agencement discret et régulier de points dans un espace. Le réseau de Leech est la généralisation en 24 dimensions au réseau que l'on obtient si l'on veut disposer de boules de rayon identique de la manière la plus efficace possible (comme le font presque certains les réseaux crystallins qui ont cependant plu s de contraintes).

Petites dimensions:

En 24 dimensions, j'imagine que c'est plus compliqué. Toujours est-il que ces objets, à l'intersection entre la géométrie, l'algèbre et la combinatoire, passionnent Conway qui est très doué pour les étudier. Il se mit dont à étudier le groupe des symétries du réseau de Leech. Par symétrie, je veux dire les transformations de l'espace à 24 dimensions parmi celles qui conservent les distances (il y a une notion de distance naturelle en dimension 24), qui laissent ce réseau invariant.
Thompson lui avait dit qu'il s'intéresserait à ce réseau si Conway arrivait à les compter, autrement dit à trouver l'ordre de ce groupe. Il y parvint: 4 157 771 806 543 630 000. Autant dire que sa méthode n'était pas celle que j'ai donnée plus haut. Apprendre ce résultat suffit à faire penser à Thompson que le groupe en question devait contenir tous les groupes de Mathieu et certains autres groupes sporadiques (sans cependant pouvoir être décomposé à l'aide de ces groupes). C'était donc, si le groupe était bien un groupe sporadique, une meilleure nouvelle pour la classification que la découverte d'un groupe entièrement nouveau. Cela suggérait que les groupes sporadiques avaient une sorte d'unité, et aussi qu'on pourrait peut-être y comprendre quelque chose.
Par la suite, Bernd Fischer découvrit deux autres groupes sporadiques, encore beaucoup plus gros, à partir de constructions de type réseau de Leech. Le plus gros d'entre eux fût baptisé le Monstre en raison de sa taille que Fischer et Conway pensaient énorme. (Tous les groupes sporadiques sont dans la table périodique en premier spoiler, avec leur ordre.)
Lorsque j'écris "découvrit", cela ne veut pas dire construisit. En 1978, les 26 groupes sporadiques avaient été découverts, au sens où des arguments convaincants de leur existence avaient été trouvés, mais pour deux d'entre eux, aucun moyen de les représenter n'avait été trouvé. Il s'agissait d'un groupe sporadique découvert par Janko, et du Monstre.
Conway avait rassemblé des propriétés du Monstre dans ce qui est maintenant appelé l'Atlas des groupes finis, encore en cours de complétion en ligne. Il savait notamment que ce groupe ne pouvait pas être représenté en moins de 196 883 dimensions.
De son côté, McKay lisait un article sur la fonction modulaire, qui est un objet important en maths, lié notamment à la preuve ultérieure par Andrew Wiles du théorème marginal de Fermat. Cette fonction est liée à une suite de nombres naturels 196 884, 21 493 760, 864 229 970,...
Comment obtenir la suite? C'est simple, il suffit de prendre les dimensions en les quelles le Monstre peut être représenté, de les additionner, et d'ajouter un. Ou plutôt, c'est ce qui fonctionne pour les premiers termes, comme l'ont remarqué McKay et Thompson. Cette relation conjecturale très étrange entre des coefficients d'une fonction en analyse complexe et les dimensions de représentation du Monstre fut baptisée "clair de lune" par Conway. Avec son collègue Simon Norton, ils la tirèrent au clair sans cependant la comprendre, et sans que cela leur permette de construire le Monstre. Plus tard, des liens ont été trouvé entre certains espaces mathématiques en théorie des corde, le Monstre, et la fonction modulaire, sans non plus qu'une explication apparaisse.
Finalement, cela sera un autre mathématicien, Bob Griess, qui arrivera à construire le Monstre. Parallèlement, l'équipe de Conway construira le dernier groupe sporadique à l'aide d'outils informatiques (aujourd'hui supplanté par la main je crois).

Dans le début des années 80, au nombreux détails de corrections d'erreurs et de lacunes près (la dernière grosse lacune trouvée, en 2004), la communauté mathématique affirmait que la classification était terminée. Les 26 groupes sporadiques étaient les seuls. Il faut savoir que l'édifice est si grand qu'il est difficile de le considérer comme un simple théorème.

Je conseille à ceux que ce genre de choses intéresse de lire le livre La Symétrie ou les maths au clair de Lune de Marcus du Sautoy. Il explique comment le problème de la CDGFS peut être vu comme le parachèvement d'une quête mathématique, entre l'algèbre et la géométrie, qui s'étend l'antiquité à notre époque. C'est le meilleur livre de vulgarisation mathématique que j'aie lu, et aussi le seul.

** précision importante: une transformation est d'un point de vue mathématique la donnée de chaque point avant et après la transformation. Deux mouvements différents qui à la fin donnent pour chaque point la même modification sont considérés égaux. Ainsi, soulever un verre vide puis le reposer tel quel revient pour nous à ne rien faire.

par paela Lun 13 Avr 2020 - 21:49

@Topsy: Je crois que j'avais lu dans La Symétrie que Conway s'était beaucoup entraîné à cet exercice et qu'il était assez fier de ses capacités, au point de se penser le plus rapide au monde à pouvoir trouver le jour de la semaine d'une date donnée.

par I am So Sure Lun 13 Avr 2020 - 22:19

A ce jour, une des meilleures dissertations autour de la notion de "Pn manipulateur" 2nd degré

.

C'est absolument passionnant. Merci !

par horizon artificiel Mar 14 Avr 2020 - 9:21

J'avais vu le jeu de la vie dans une vidéo de science étonnante.
C'est vraiment surprenant et fascinant de voir les animations, et les noms des motifs.....

https://www.youtube.com/watch?v=S-W0NX97DB0

par tim9.5 Mer 15 Avr 2020 - 15:32

Bravo Paela pour ta présentation. Quel travail ! C'est la première fois que tu écris un tel article de qualité sur ZC ? Youpi !

Pour aider à la lecture de ton texte, je me permets de rajouter quelques éléments.

1) La notion de groupe est lié au personnage du XIXe siècle, Evariste Galois. HP avant l'heure, ayant sauté une classe puis redoublé, excellent dans les branches qui l'intéressaient, se penche alors sur les mathématiques, manuscrits perdus, théorie incomprise par les mathématiciens de l'époque, prison, mort d'un duel au pistolet pour les yeux d'une gente dame. On en a fait le prototype du mathématicien romantique incompris et génial.

2) Etudier les groupes, c'est faire "simplement" de la grammaire.
a) On part d'une phrase "les chatons sont blancs". On procède a une première abstraction : "les chatons" sont le sujet du verbe. Du moment qu'on a défini correctement les mots "sujet" et "verbe", on peut rechercher ces termes dans n'importe quelle phrase : "les fioles sont remplies",etc. (voir wiki).
b) Deuxième niveau d'abstraction : on cherche cette fois-ci les propriétés mots "sujet" et "verbe". A ce stade, on laisse de côté les phrases de départ, mais on y revient souvent pour vérifier que ça fonctionne. Exemple de propriété : "un verbe au pluriel possède un sujet au pluriel, donc on met un "s" à chatons, fioles, etc. On peut penser aussi "s" comme un invariant : si je remplace dans notre cas le sujet par il ou elle, je mets s à la fin. Le "s" de chatons se retrouve dans le "ils". Puis on cherche les exceptions : "x" dans oiseaux devient "s" dans ils. En résumé, faire de la grammaire, c'est abstraire de l'abstraction. Deuxième niveau d'abstraction.

Paela cite plusieurs groupes (premier niveau d'abstraction), dans l'ordre :

a) Les entiers relatifs (...,-4,-3,-2,-1,0, 1, 2, 3, 4 ...) avec l'opération +.
Est-ce que ça forme un groupe (premier niveau d'abstraction)? Il suffit de reprendre la définition de groupe donné au début de son texte:
i) un entier relatif + un entier relatif donne encore un entier relatif
ii) est-ce qu'il existe un entier relatif a tel que -4 + a = -4 ? Oui, c'est 0 et ça marche avec tout nombre relatif
iii) est-ce qu'il existe un entier relatif b tel que 4 + b = 4? Oui ,c'est -4 qui est aussi un nombre relatif.
iv) prenons trois nombres relatif (-2), 3 et 5. Est-ce qu'en additionnant d'abord les premiers nombres (-2) et 3, ou les deux derniers (3 et 5), le résultat reste le même? Oui (-2 + 3 )+ 5 = 1+5 = 6 = -2 +8 = -2 + (3 +5).

b) Les déplacements d'un carré sur lui-même forment un groupe. Un groupe de mouvement plus simple se trouve sur http://villemin.gerard.online.fr/Referenc/Outils/AOUTILS/GrouIntr.htm#quartavec des images.

c) le groupe des permutations (des 4 chanteurs).

Paela passe ensuite à la grammaire (les propriétés de groupe, deuxième niveau d'abstraction) : le tableau des groupes finis, avec ses propriétés et ses invariants.

En passant,

D'autres mathématiciens prouvèrent l'existence, depuis construisirent d'autres groupes sporadiques, jusqu'à ce qu'il y en ait onze au total.

C'est une phrase type du mathématicien : je sais que ça existe et je peux le prouver, mais je ne sais pas à quoi ça ressemble. Etonnant !

Troisième étape : appliquer la classification des groupes (la grammaire) dans d'autres contextes.
Un exemple frappant, en dehors de la théorie des groupes, est celui d'Emmy Noether, qui d'un théorème abstrait , permet de poser les bases solides de la physique , en "faisant le lien entre symétries et lois de la conservation" de la physique (wiki).

Dernière remarque : quand on parle de "simplicité" en math, ça signifie écrire de manière compacte comme un haïku. Les intitulés de math sont plutôt proches de la poésie, et parfois les démonstrations des romans. Ca ne veut pas dire que c'est simple, mais élégant !

Voilà voilà.

par Invité Mer 15 Avr 2020 - 16:05

Salut tim9.5

Jolie démonstration, mais je me demande s'il n'y a pas une erreur là

iii) est-ce qu'il existe un entier relatif b tel que 4 + b = 4? Oui ,c'est -4 qui est aussi un nombre relatif.

par tim9.5 Mer 15 Avr 2020 - 16:13

Bien vu ! C'est 4 + b = 0.

par Topsy Turvy Mer 15 Avr 2020 - 16:21

J'aurais encore précisé qu'Évariste Galois est mort à ± 20 ans et demi.
Je connais pas grand chose en math, mais l'âge du décès de Galois, oui.
:rigole:

Merci pour toutes ces présentations, ça me plaît beaucoup...

par Sélène-Nyx Mer 15 Avr 2020 - 19:33

John H.Conway, j'connais pas, ni ses travaux … Crying or Very sad

Normal, j'n'aime pas les sciences …

Quand à Evariste Galois, j'ai gardé le souvenir d'un jeune prodige, saint-simonien, opposant à Louis-Philippe (d'où le duel), qui, prévoyant sa mort le lendemain, avait passé sa nuit à écrire son "testament mathématique", retrouvé 10 ans après… Et qui aurait pu ne jamais être retrouvé.
Sa prémonition et a volonté à laisser une trace de ses travaux, m'ont toujours impressionnée …. (Mais je ne connais rien de ses travaux, sinon qu'ils se sont révélés d'une importance capitale …. Bien que décriés de son vivant.

"Nul n'est prophète en son pays"!

par paela Mer 15 Avr 2020 - 20:08

Merci pour les compléments tim95. J'ai hésité à mettre des illustrations d'autres exemples mais je trouvais le message déjà assez lourd. Il faudrait aussi que je corrige quelques erreurs ou typo. C'est probablement la première fois que j'écris de moi-même un truc en rapport avec les maths sur ZC, et il ne faut pas voir ça comme le début d'une longue série (mais je ferai au moins les nombres surréels ici).

@horizon artificiel: Parfait, comme ça je n'aurai pas à le faire. Je n'ai pas vu la video mais j'ai trouvé celles que j'ai vues de cette chaîne étaient très bien!

@Sélène-Nyx: Je crois que c'est une présentation qui tire un peu trop du côté de l'image du génie incompris. Les travaux de Galois n'étaient pas vraiment décriés de son vivant.
Cependant je partage ton impression. Se retrouver face au constat que sa vie serait peut-être courte, et qu'une partie de son temps devrait se retrouver consacrée à la présentation de ses idées pour la postérité... Je me demande ce comment il a vécu les jours qui ont précédé le duel.

par paela Lun 27 Avr 2020 - 23:28

Les nombres surréels maintenant. Je vais faire ça en plusieurs parties pour qu'il soit possible d'y comprendre quelque chose. La première maintenant, les autres plus tard. Je mets tout cela sous la forme images jpg car écrire des maths sur le forum est pénible et je suis beaucoup plus rapide avec les bons outils.

Nombres surréels

Les nombres surréels sont des objets mathématiques qui se comportent un peu comme les nombres réels. Plutôt que de les voir comme une généralisation des nombres réels, je préfère considérer la classe No des nombres surréels comme un terrain de jeu et d'expérimentation mathématique avec des contraintes simples: de l'ordre et de l'ordre!
Avant de parler de nombres surréels, il faut parler des nombres réels. On pourra dans la suite voir en quoi les nombres surréels sont issus d'un mariage, sous la bénédiction de Conway, des (idées de) coupures de Richard Dedekind et des ordinaux de Georg Cantor.

I - Le continuum réel par les coupures de Dedekind:

par Topsy Turvy Mar 28 Avr 2020 - 0:02

C'est beau comme du LaTeX, ça doit être du LaTeX.
Faudrait vraiment que j'apprenne à utiliser ce truc.
[Si vous avez des conseils pour débutants, I'm in.]

par paela Mar 28 Avr 2020 - 0:20

Ce n'est pas du LaTeX, c'est du TeXmacs. Beaucoup plus simple à utiliser mais beaaaauucoup moins utilisé, donc moins pratique pour communiquer.

edit: Par curiosité, j'ai cherché, et oui, il y a quelques vidéos d'un créateur de TeXmacs qui présentent certaines fonctionnalités. Trois exemples plus bas pour se donner une idée.

Ecrire votre premier article avec TeXmacs:

Conversion automatique TeXmacs-> LaTeX:

Ecrire des formules mathématiques simples:

par Topsy Turvy Mar 28 Avr 2020 - 0:42

Ah, merci, je retiens l'idée, cool !

par Invité Mar 28 Avr 2020 - 8:38

La suite, la suite... Very Happy

Spoiler:

par paela Mar 28 Avr 2020 - 20:22

Merci pour tes commentaires Yop, je corrigerai quand je ferai la suite.

par siamois93 Mar 28 Avr 2020 - 21:22

Merci Paela, c'est super intéressant.

par tim9.5 Mer 29 Avr 2020 - 17:11

Excellent article. Il y a un côté apaisant de lire des mathématiques. Quelques notions de bases, puis déploiement de leurs richesses, de manière calme et logique.
Bravo aussi pour ta manière de présenter l'affaire avec TeXmacs. Je retiens l'idée, quand j'aurai le courage de me lancer dans l'intrication quantique...

par paela Ven 15 Mai 2020 - 19:58

Hier j'ai rencontré Conway. On était à une conférence dans ce qui ressemblait à une salle de collège mais c'était assez lumineux donc c'était sympa. Je crois qu'on était quelque part dans la jungle. Ne faîtes pas mon analyse s'il vous plaît.
Donc je m'assois juste devant lui (mon subconscient ne l'ayant pas encore transformé en Conway) un peu avant le début du prochain exposé. Il commence à me parler des nombres surréels (!). Jusque là c'est assez réaliste. Je me rends compte que c'est John Conway avec un H au milieu mais je fais semblant de ne pas être surpris (<--réalisme). Il m'explique qu'en ce moment il se dit qu'il s'y est mal pris avec les nombres surréels, qu'en fait il faut les voir comme des jeux à trois joueurs qui à chaque partie font appels à trois coéquipiers, et ainsi de suite. En faisant, ça, on obtient une formule (qu'il écrit sur le mur tel un mathématicien de film) du genre l(x) = x+a(x) où il explique que a(x) s'interprète comme "l'aire" du nombre surréel.
Je lui dis que je m'intéresse aux nombres surréels, et il me demande de réfléchir à une généralisation avec un volume. On réfléchit un moment, et on trouve une formule du genre l(x)= x+v(x). Ne cherchez pas à comprendre c'est de la logique de rêve. On est assez content, mais c'est de courte durée car je suis violemment tiré du sommeil par mon réveil. Adieu à jamais Conway.

Voici la contribution du jour. Le prochain chapitre sur les nombres surréels sera pour la prochaine fois.

par paela Jeu 21 Mai 2020 - 12:33

Avant de parler des nombres surréels, il est utile d'en apprendre un peu sur les structures inductives, les preuves par induction, et les ordinaux. Il est possible de dire des choses intéressantes sur les surréels sans faire ce travail: la définition de Conway est en deux phrases, et il y a un livre de vulgarisation sur les surréels qui je pense ne rentre pas dans les détails.
Mais d'une part avoir une idée même basique de ce que sont les ordinaux peut quand-même aider, d'autre part la définition de Conway peut sembler "être de la triche" si on ne connait pas les structures inductives, c'est d'ailleurs volontaire de la part de Conway.

Donc bref, vous n'êtes pas obligés de comprendre ce qui suit pour comprendre les nombres surréels qui viendront après, mais si vous ne captez-pas alors, ce sera une bonne idée de revenir ici.

II - Choses inductives:

par fift Jeu 21 Mai 2020 - 12:56

Je poste un petit message, juste pour suivre et y revenir après parce que ça me paraît super intéressant.

par tim9.5 Sam 23 Mai 2020 - 17:23

Super paela !
J'ai quelques notes de lectures à te partager.

1) Je n'ai pas bien compris la signification de classe, il me manque un exemple concret.

2) dans "5. Structures inductives", il y a utilisation de O et de OC. J'en déduis que c'est pareil, n'est-ce pas?

3) dans "6. Exemples", le rang est de 4, et sa taille est de 11, pour la proposition non(A4 ou non(A1 ou A4)). Je ne suis pas sûr de calculer correctement le rang, quand à la taille, c'est un mystère pour moi.

Voilà voilà Wink

par paela Sam 23 Mai 2020 - 23:09

Salut tim9.5 et merci pour les notes!

1) Il n'y a pas de différence conceptuelle entre les classes et les ensembles. Dans la théorie dite naïve des ensembles, on considérait que si P(x) était un prédicat (une propriété) portant sur un truc auquel la variable x fait référence, alors il existait un ensemble dont les éléments sont les objets a qui satisfont P(a). Dans cette théorie, les classes et les ensembles sont unifiés, ou disons il n'y a pas de classe. Russell a montré que cette théorie était contradictoire, en remarquant que l'ensemble A qui correspond à la propriété P(x): "x n'appartient pas à x" posait problème. Le problème est qu'il y a équivalence entre "A appartient à A" et le contraire, c'est-à-dire "A n'appartient pas à A". Ce n'est rien d'autre que le paradoxe du menteur, du barbier, de "cette phrase est fausse", sauf qu'en maths il y a des contextes comme celui-ci où cela a un sens clair de dire "cette phrase est fausse". Heureusement depuis le paradoxe de Russell, ces contextes ont toujours demandé une hypothèse supplémentaire et les raisonnements correspondants ont servi à démonter les hypothèses en question.
Donc ensuite on a restreint cette règle prédicat --> ensemble en imposant en gros que le prédicat P(x) impose déjà que x appartient à un ensemble donné avec le prédicat. L'axiome correspondant s'appelle "axiome de compréhension" ou "axiome de séparation". Dans la théorie des ensembles normale, le raisonnement de Russell sert à montrer qu'il n'y a pas d'ensemble qui contient tous les ensembles, car sinon l'axiome de compréhension permettrait de recréer l'ensemble A de tout à l'heure. Mais on aimerait quand même parfois parler d'un "truc" qui contient tous les ensembles, en fait on aimerait bien pouvoir "un peu" parler de certains prédicats comme des objets normaux (comme des ensembles). C'est d'ailleurs cette capacité de transformer des propriétés, des abstractions ou des notions "méta" en objets basiques qui fait la puissance des mathématiques.
Donc on appelle classe le "truc" qui correspond à un prédicat, et on dit que a est dans la classe qui correspond à P(x) si P(a) est vrai.
Un autre exemple de classe qui n'est pas un ensemble est la classe Ord des ordinaux. La raison est que pour tout ordinal α, on a par définition que "α n'appartient pas à α". Si Ord était un ensemble, alors ça serait un ordinal (cela se vérifie assez facilement). On aurait donc "Ord appartient à Ord" parce que le Ord de droite contient tous les ordinaux y-compris celui de gauche, et "Ord n'appartient pas à Ord" à cause de l'argument précédent: problématique.
Un autre exemple sera la classe des nombres surréels, qui si elle était un ensemble imposerait l'existence d'un nombre surréel strictement plus grand que lui-même. Toujours le même genre de contradiction de type diagonal donc.

2) Oui j'avais noté O au début puis OC, et j'ai dû laisser traîner des O. Je corrigerai la prochaine fois.

3) Par taille ici je veux dire la longueur du mot vu comme suite de symboles: ici le nombre d'occurrences cumulées de "non", "(", ")", "A_4", "ou", et "A_1".
Pour ce qui est du calcul du rang, en général ce n'est pas facile. La technique en général est de regarder si un élément est dans I_0, si oui stopper et renvoyer 0. Sinon regarder s'il est dans I_1, si oui stopper et renvoyer 1, etc... Bien sûr le problème "regarder s'il est dans I_n" peut être impossiblement compliqué s'il n'y a d'autre méthode que de faire la liste (potentiellement infinie) des éléments de I_n.
Mais dans le cas des formules propositionnelles et de beaucoup de langages construits inductivement, il y a un truc qui fait tout fonctionner, y compris les définitions inductives. Je ne l'ai pas écrit explicitement, mais il y a un théorème de lecture ou d'écriture unique, qui dit en gros que toute formule propositionnelle est obtenue de manière unique dans la construction inductive.
On peut voir que le rang d'une formule propositionnelle se calcule inductivement avec les règles
r(non F)=1+r(F);
r((F ou G)) = 1+ max(r(F),r(G)); et
r((F et G)) = 1 + max(r(F),r(G)).
En appliquant ça à cette formule de taille onze tu obtiens 4.

Ce que je voulais dire avec ce passage c'est que si on prend un mot au hasard, il n'est pas facile en le lisant dans la longueur de savoir s'il est bien construit, et c'est encore plus difficile de donner les règles de construction des bons mots en termes de conditions données progressivement sur chaque lettre du mot. Le langage des bons parenthésages, est obtenu avec I = vide et deux opérations (sans condition) qui sont prendre un mot m et le mettre entre parenthèses (m), et prendre deux mots m et n et les concaténer en mn. C'est le langage des bonnes façons de mettre des parenthèses. Ex (()())() est un bon parenthésage qu'on peut décorer en ((1+1)x(2+3))+(3x7) si l'on veut. (()( n'en est pas un clairement.
Dans ce langage on peut savoir en lisant de gauche à droite (ou l'inverse) si un mot est bien parenthésé: s'il est vide c'est bon. Sinon il doit commencer par (. On note o le nombre de parenthèses ouvrantes en réserve et on commence avec o=1. On se déplace vers la droite, à chaque fois qu'on trouve ( on ajoute 1 à o, et à chaque fois qu'on trouve ) on retranche 1 à o. La partie est gagnée (le parenthésage est bon) si o=0 une fois arrivé à la dernière lettre du mot. Donc voilà c'est un exemple où on peut dire simplement comment reconnaître les bons et les mauvais mots.

par horizon artificiel Dim 7 Juin 2020 - 4:58

Coucou:

par paela Dim 7 Juin 2020 - 12:54

nombres naturels, ordinaux, cardinaux, cardinalité:

par horizon artificiel Lun 8 Juin 2020 - 0:55

Encore besoin de quelques précisions....:

par paela Ven 12 Juin 2020 - 13:50

Spoiler:

par horizon artificiel Ven 12 Juin 2020 - 15:09

Il n'y a rien de sec dans ta réponse.
Ce sont des précisions de vocabulaire dont j'avais besoin pour bien classer tout ça dans ma tête.
Ce que je vais donc pouvoir faire
Je te remercie Very Happy

par paela Jeu 15 Oct 2020 - 20:26

Les nombres surréels pour conclure ces présentations.

III - Nombres surréels:

Il y a un bouquin de Donald Knuth (qui a inventé le nom "nombre surréel" alors que Conway parlait seulement de nombres), qui présente de manière romancée et vulgarisée (plutôt romancée que vulgarisée) la découverte des nombres surréels par deux étudiants sur une île je crois. Je ne l'ai pas lu mais ça a l'air bien et a priori facile à lire. Il s'appelle Surreal Numbers: How Two Ex-students Turned on to Pure Mathematics and Found Total Happiness : a Mathematical Novelette et ça existe en français.

par horizon artificiel Mer 28 Avr 2021 - 0:17

Spoiler:

------------

edit

Paradoxe de Zénon....:

par paela Mer 28 Avr 2021 - 17:01

@horizon artificiel: Les remarques de Dehornoy sont d'ordre métaphysique ou métamathématique. Dans une démonstration mathématique, on utilise des abréviations qui doivent être définies car justement "2" n'est pas donné à l'avance comme entité. A ce moment là ce n'est pas que 2 est l'ensemble {0,{0}} (ou un autre avatar), mais que c'est de cet ensemble qu'on parle lorsqu'on écrit 2. En pratique tout le monde s'en moque de savoir ce que 2 signifie car on sait qu'on a souvent un 2 qui existe là où on en a besoin. De même, savoir si N = omega ou pas n'est pas important car on pourrait choisir N et omega différemment sans rien changer aux maths (c'est principalement ce que dit Dehornoy). Par contre il y a une convention plutôt partagée qui est que N, omega et aleph_0 sont la même chose.

Pour la flèche, on peut convenir que l'ensemble des positions de la pointe est représenté par l'ensemble des nombres entre 0 et 1. Et que l'ensemble des positions de la flèche aux dates 0s, 0.9s, 0.99s, etc... est l'ensemble des nombres 0, 0.9, etc... (en normalisant pour que la flèche arrive en 1 à 1s). Cet ensemble est alors de même cardinal que N, et puisque l'application 0 --> 0; 1 --> 0.9; 2 --> 0.99; etc est une bijection strictement croissante, l'ordinal correspondant est omega (qui est égal à N).
A mon avis, cela ne va pas t'aider à comprendre de chercher à percer le mystère de la ressemblance entre N, omega et aleph_0 (qui comme dit plus haut est une affaire de convention); en revanche le vrai contenu des notions de cardinal et d'ordinal se trouve dans les définitions de ces notions, par exemple sur Wikipedia.

Il n'y a pas de lien conventionnel entre N et le symbole oo qui est juste un symbole qui apparaît souvent en maths. La notation "oo/oo=indéterminé" est un artefact utilisé par les profs de maths pour tenter de détourner leurs élèves de la tentation de dire "si f et g tendent vers +oo alors f/g tend vers 1" (puisque ce dont tu parles en est un contre-exemple). Lorsqu'on dit qu'une fonction f tend vers +oo, on définit ainsi la notion de limite (infinie) seulement. le symbole oo lui-même n'est qu'un des termes de cette expression, à peu près au même titre que "t" est un des caractères du mot "tigre".
Donc interlocuteur mathématicien ne sait probablement pas comment interpréter les différentes occurrences de oo dans ce que tu rapportes, avant même de pouvoir savoir si c'est vrai.

par horizon artificiel Mer 28 Avr 2021 - 23:35

Spoiler:

par paela Jeu 29 Avr 2021 - 14:26

Oui mais même dans une convention un symbole représente quelque chose.

Oui, et on dit qu'une fonction tend vers l'infini et non vers le tigre pour une raison (d'où mon "à peu près"). Le point important est que la définition d'une expression composée ne détermine pas toujours le sens des termes qui la composent.

Est-ce dans N, je peux dire que si j'ai une fonction f qui tend vers oo (+oo si tu préfères mais je suis dans N), alors cet infini est omega ou pas ?
oo ne serait qu'une dimension de l'infini dans un ensemble.....

La réponse courte est que comme le symbole oo n'est pas défini, savoir s'il a un lien avec (sans parler d'être) omega n'a pas de sens et tu ne serais pas avancée d'un pouce si je te disais "oui" ou "non".

On peut si l'on veut faire un lien entre la notion de limite à l'infini et l'infini quantifié avec les ordinaux (c'est plus ou moins mon sujet de thèse). Si tu veux réfléchir à ce genre d'idée, tu peux considérer le problème suivant, qui est un problème ouvert en logique soulevé par Skolem il y a environ soixante ans.

Un problème de Skolem:

par horizon artificiel Jeu 29 Avr 2021 - 22:08

Très intéressant Very Happy

Cette affaire d'infini et de dénombrable, ça me fait penser au problème de la vitesse limite de la lumière et au problème de l'additivité des vitesses...

Merci pour ton éclairage qui n'en est pas un Wink

tu ne serais pas avancée d'un pouce si je te disais "oui" ou "non"

mais qui m'éclaire sur l'absence de nécessité de recherche de sens en logique pure.....

Spoiler:

par Topsy Turvy Mer 22 Sep 2021 - 13:49

Article ludique dans Pour la science (entier pour abonnés) :

Cinq pépites mathématiques de John Conway
Le grand mathématicien britannique vient de disparaître. Pour lui rendre hommage, voici un petit échantillon de mathématiques comme les aimait ce magicien des jeux et des nombres.
Jean-Paul Delahaye 25 août 2020 Pour la science N° 515
[...]
https://www.pourlascience.fr/sr/logique-calcul/cinq-pepites-mathematiques-de-john-conway-19963.php

Repris ici dans Scientific American :
https://www.scientificamerican.com/article/for-math-fans-some-puzzles-from-game-of-life-creator-john-conway/

par Invité Sam 16 Avr 2022 - 17:54

En février 2020, la mathématicienne Lisa Piccirilo a mis fin à une énigme datant des années 70 en démontrant que le noeud de Conway n'était pas à bord régulier.

John H. Conway est malheureusement décédé avant la parution des travaux de Lisa Piccirillo (la validation par les pairs a duré deux ans)...

Une vidéo en français à ce sujet : https://yewtu.be/watch?v=gz-MN3s-jcQ

Le premier commentaire sous la vidéo fournit des liens très intéressants pour qui veut creuser y compris celui qui pointe vers l'article de Lisa Piccirilo.