Accueil
Évènements
Rechercher
S'enregistrer
ConnexionTenseurs
3 participants
Page 1 sur 1
Tenseurs
par Invité Ven 8 Jan 2016 - 23:27
Edit : ce sujet est issu d'un scission avec un autre sujet. Le message initial était le suivant:
- Spoiler:
- prométhéus a écrit:Une vidéo très pédagogique sur les tenseurs:
- Spoiler:
Exemples en physique
En physique, un exemple simple : considérons un bateau flottant sur l'eau. On veut décrire l'effet de l'application d'une force sur le déplacement du centre du bateau dans le plan horizontal.
La force appliquée peut être modélisée par un vecteur, et l'accélération que subira le bateau par un autre vecteur. Ces deux vecteurs sont horizontaux. Mais leurs directions, qui devraient être identiques pour un objet de forme ronde, ne le sont plus pour un bateau, qui est plus allongé dans un sens que dans l'autre. La relation entre les deux vecteurs, qui n'est donc pas une relation de proportionnalité, est cependant une relation linéaire, au moins si on considère une force petite.
Une telle relation peut être décrite en utilisant un tenseur de type (1,1) (1 fois contravariant, 1 fois covariant). Un tel tenseur peut être considéré comme une application linéaire qui transforme un vecteur du plan (la force) en un autre vecteur du plan (l'accélération). Dans une base donnée, ce tenseur peut être représenté par une matrice, qui, lorsqu'on la multiplie par les composantes d'un vecteur, donne les composantes d'un autre vecteur. De la même manière que les nombres qui représentent un vecteur changent quand on change de système de coordonnées, les nombres qui représentent le tenseur dans la matrice changent quand le système de coordonnées change.
En mécanique, on peut également décrire les tensions, les forces intérieures subies par un solide ou un fluide par un tenseur.
Le mot tenseur vient effectivement du verbe tendre, qui signifie soumettre à une tension. Considérons un élément de surface à l'intérieur du matériau ; les parties du matériau situées d'un côté de la surface exercent une force sur l'autre côté de la surface (et réciproquement). En général, cette force n'est pas orthogonale à la surface, mais dépendra linéairement de l'orientation de la surface.
Nous pouvons la décrire par un tenseur d'élasticité linéaire, tenseur de type (2,0) (2 fois contravariant, 0 fois covariant), ou plus précisément, par un champ de tenseurs de type (2,0), puisque les forces de tension varient de point à point.
suite sur : https://fr.wikipedia.org/wiki/Tenseur
(donc ici on ne peut pas utiliser l'expression "eh ta soeur elle fait du bateau" par exemple ?)
et c'est en lien avec ça ? (pour l'instant je n'ai compris que Sinus
et parce que j'ai de la sinusite).
Vous comprenez tout ça ?
(cela dit tout le monde a pensé à mettre une pompe, mais pas un rameur qui là à l'instant T m'aurait été bien utile comme émoticône 
)
Invité- Invité
Re: Tenseurs
par Invité Sam 9 Jan 2016 - 21:50
Les tenseurs ? Oui, ça fait partie de la base des maths nécessaires pour commencer à faire un peu de physique. Disons que ce que tu as marqué dans ton post me parait une très mauvaise manière de vulgariser ce qu'est un tenseur. Si tu ne sais pas ce que c'est, inutile de commencer à essayer de savoir ce qu'est un tenseur contravariant, covariant, antisymétrique et j'en passe. Déjà savoir ce que c'est c'est la base, ses propriétés, c'est l'approfondissement.
Non, un tenseur c'est un truc tout bete en fait, on en fait tout un pataquès, on peut s'amuser à complexifier la chose dans tous les sens pour se la péter, mais c'est simple en fait.
Tu prends un cube, et sur chaque face tu exerces une force. Sur chaque face du cube, tu as une force différente. Une force c'est un vecteur, donc sur chazque direction X,Y,Z du cube, tu auras une force qui a 3 composantes. Pour symboliser cette contrainte, on utilise un tenseur 3x3, qui pour chaque direction du cube te donne le vecteur force qui est exercé. Voilà, c'est tout. C'est le tenseur des contraintes qui est un tenseur 3x3.
Non, un tenseur c'est un truc tout bete en fait, on en fait tout un pataquès, on peut s'amuser à complexifier la chose dans tous les sens pour se la péter, mais c'est simple en fait.
Tu prends un cube, et sur chaque face tu exerces une force. Sur chaque face du cube, tu as une force différente. Une force c'est un vecteur, donc sur chazque direction X,Y,Z du cube, tu auras une force qui a 3 composantes. Pour symboliser cette contrainte, on utilise un tenseur 3x3, qui pour chaque direction du cube te donne le vecteur force qui est exercé. Voilà, c'est tout. C'est le tenseur des contraintes qui est un tenseur 3x3.
Invité- Invité
Re: Tenseurs
par Invité Mar 12 Jan 2016 - 22:38
hobb a écrit:Les tenseurs ? Oui, ça fait partie de la base des maths nécessaires pour commencer à faire un peu de physique. Disons que ce que tu as marqué dans ton post me parait une très mauvaise manière de vulgariser ce qu'est un tenseur. Si tu ne sais pas ce que c'est, inutile de commencer à essayer de savoir ce qu'est un tenseur contravariant, covariant, antisymétrique et j'en passe. Déjà savoir ce que c'est c'est la base, ses propriétés, c'est l'approfondissement.
Non, un tenseur c'est un truc tout bete en fait, on en fait tout un pataquès, on peut s'amuser à complexifier la chose dans tous les sens pour se la péter, mais c'est simple en fait.
Tu prends un cube, et sur chaque face tu exerces une force. Sur chaque face du cube, tu as une force différente. Une force c'est un vecteur, donc sur chazque direction X,Y,Z du cube, tu auras une force qui a 3 composantes. Pour symboliser cette contrainte, on utilise un tenseur 3x3, qui pour chaque direction du cube te donne le vecteur force qui est exercé. Voilà, c'est tout. C'est le tenseur des contraintes qui est un tenseur 3x3.
- Spoiler:
Hello, merci de ta réponse. je n'ai surtout voulu rien du tout mais surtout tout l'inverse. Ca m'avait juste faire prendre encore plus acte de qui peut se trouver ici. et dans le bon sens.
Je ne me sentirais pas autorisée à vulgariser ce que je ne connais ni ne maîtrise.
C'était ma façon de le dire mais y'a des mots qui parlent même si on n'y connaît c'est toujours intéressant de s'intéresser à d'autres choses que les siennes et ça enrichit aussi le vocabulaire et ça peut à mes yeux permettre d'imager.
Merci de ton explication. en tous les cas.
J'ai eu envie de rajouter qu'en fait le fait d'une présentation que j'appellerais par le bas montre ou m'a montré un tas de choses sur la surdouance. Non pas que je ne pensais pas que.... mais ça parle autrement de la surdouance. Les deux points sont intéressants du coup. Merci de m'avoir donné un sujet de réflexion, en plus.
Invité- Invité
Re: Tenseurs
par Invité Mer 13 Jan 2016 - 12:03
Ha mais ce n'est pas une accusation envers toi, c'est juste que les liens que tu as mis ne me semble pas les plus indiqués pour apprendre ce que c'est, c'est tout ;-)
Invité- Invité
Re: Tenseurs
par Invité Mer 13 Jan 2016 - 12:10
hobb a écrit:Ha mais ce n'est pas une accusation envers toi, c'est juste que les liens que tu as mis ne me semble pas les plus indiqués pour apprendre ce que c'est, c'est tout ;-)
Pas de souci, je ne l'ai pas pris comme ça. et j'ai bien pris note dans le bon sens des conseils que tu m'as donnés.
Invité- Invité
Re: Tenseurs
par prométhéus Jeu 24 Mar 2016 - 23:10
Wikipédia transposé à la gastronomie, c'est un peu le guide michelin, agrémenté de photos couleurs de vomis pour faire la mise en bouche des restaurants.Natatypique a écrit:
- Spoiler:
Exemples en physique
En physique, un exemple simple : considérons un bateau flottant sur l'eau. On veut décrire l'effet de l'application d'une force sur le déplacement du centre du bateau dans le plan horizontal.
La force appliquée peut être modélisée par un vecteur, et l'accélération que subira le bateau par un autre vecteur. Ces deux vecteurs sont horizontaux. Mais leurs directions, qui devraient être identiques pour un objet de forme ronde, ne le sont plus pour un bateau, qui est plus allongé dans un sens que dans l'autre. La relation entre les deux vecteurs, qui n'est donc pas une relation de proportionnalité, est cependant une relation linéaire, au moins si on considère une force petite.
Une telle relation peut être décrite en utilisant un tenseur de type (1,1) (1 fois contravariant, 1 fois covariant). Un tel tenseur peut être considéré comme une application linéaire qui transforme un vecteur du plan (la force) en un autre vecteur du plan (l'accélération). Dans une base donnée, ce tenseur peut être représenté par une matrice, qui, lorsqu'on la multiplie par les composantes d'un vecteur, donne les composantes d'un autre vecteur. De la même manière que les nombres qui représentent un vecteur changent quand on change de système de coordonnées, les nombres qui représentent le tenseur dans la matrice changent quand le système de coordonnées change.
En mécanique, on peut également décrire les tensions, les forces intérieures subies par un solide ou un fluide par un tenseur.
Le mot tenseur vient effectivement du verbe tendre, qui signifie soumettre à une tension. Considérons un élément de surface à l'intérieur du matériau ; les parties du matériau situées d'un côté de la surface exercent une force sur l'autre côté de la surface (et réciproquement). En général, cette force n'est pas orthogonale à la surface, mais dépendra linéairement de l'orientation de la surface.
Nous pouvons la décrire par un tenseur d'élasticité linéaire, tenseur de type (2,0) (2 fois contravariant, 0 fois covariant), ou plus précisément, par un champ de tenseurs de type (2,0), puisque les forces de tension varient de point à point.
suite sur : https://fr.wikipedia.org/wiki/Tenseur
(donc ici on ne peut pas utiliser l'expression "eh ta soeur elle fait du bateau" par exemple ?)
et c'est en lien avec ça ? (pour l'instant je n'ai compris que Sinus
Vous comprenez tout ça ?
Il y a plusieurs façons d'approcher ses bêtes que sont les tenseurs, comme l'a dit Hobb cela fait parti du bagage minimal en physique, on le trouve aussi beaucoup en Mathématiques .
Si tu as déjà rencontré les vecteurs, que l'on peut mentalement se représenter comme une flèche donc un objet possédant les informations : longueur, sens et direction
Ce vecteur peut se décomposer dans une base
- Spoiler:
[a,b] sont les composantes de v dans (u1,u2) :
v= a*u1 + b*u2
Mais cet objet existe intrinsèquement de toute base définie, de la même façon que les différentes positions d'une mouche dans l'espace, peuvent être défini dans l'espace via un repère que l'on aura défini, mais objectivement un autre repère est tout à fait possible,
ce qui défini l'objet ce n'est ni les composantes, ni la base, mais l'objet composé des deux , c'est l'idée qui est a l'origine de la notion de tenseur,
l'histoire se serait arrêtée là, si la réflexion ne s'était arrêtée qu'à ces objets, mais il en est tout autant de même d'une droite, de courbes diverses, surfaces et donc une généralisation, des composantes qui deviennent des tableaux à plusieurs indices , des bases associées ,
rien de bien compliqué en fait .
Bon c'est qu'une esquisse
prométhéus- Messages : 361
Date d'inscription : 26/04/2015
Age : 43
Localisation : troisième planète du système solaire
Re: Tenseurs
par Badak Jeu 24 Mar 2016 - 23:55
Prometheus racontre très bien mathématiquement l'idée de base de ce qu'est un tenseur.
Je vais essayer de rajouter encore un peu de sens physique.
Si on mesure des quantités physiques suivant différentes directions, c'est comme des flêches auxquelles on associe une valeur numérique (qu'on appelle une composante). Les flêches initiales: on dit qu'elles forment une base de vecteurs.
Sur un espace "plat" (comme une feuille de papier) , en général, on peut rejoindre n'importe quel point en mettant plusieurs de ces flêches bout à bout. C'est une façon de mesurer des distances, ou d'autres quantités physiques, sur l'espace en question, comme si on prenait une régle différentes pour chacun des directions choisies.
La distance mesurée restera aussi la même si on change les unités et les directions de la bonne façon: par exemple tourner les deux vecteurs de la base du même angle ne change pas les distances.
Donc les tenseurs servent à mesurer des quantités d'une manière qui ne dépend pas exactement du système d'unité et de la base de vecteurs choisie:
Si maintenant l'espace n'est pas le même dans toutes les directions, par exemple s'il est courbe comme sur la surface de la Terre, ou si certaines directions sont privilégiées par rapport à d'autres, on doit mesurer les quantités dans toutes les directions.
Sur la terre, par exemple, marcher 1000 km vers l'est, 1000 km vers le Nord, 1000 km vers le Sud, et enfin 1000 km vers Ouest ne nous permet pas de revenir au point initial à cause de la courbure terrestre: D'où l'importance de tenir compte de la direction de la mesure. C'est là que le tenseur est interessant.
C'est similaire dans un cristal où la conductivité serait plus forte suivant certaines directions que d'autres: cela va affecter la manière dont le courant électrique va vouloir circuler: on a alors un tenseur de conductivité plutôt que juste un nombre.
Je vais essayer de rajouter encore un peu de sens physique.
Si on mesure des quantités physiques suivant différentes directions, c'est comme des flêches auxquelles on associe une valeur numérique (qu'on appelle une composante). Les flêches initiales: on dit qu'elles forment une base de vecteurs.
Sur un espace "plat" (comme une feuille de papier) , en général, on peut rejoindre n'importe quel point en mettant plusieurs de ces flêches bout à bout. C'est une façon de mesurer des distances, ou d'autres quantités physiques, sur l'espace en question, comme si on prenait une régle différentes pour chacun des directions choisies.
La distance mesurée restera aussi la même si on change les unités et les directions de la bonne façon: par exemple tourner les deux vecteurs de la base du même angle ne change pas les distances.
Donc les tenseurs servent à mesurer des quantités d'une manière qui ne dépend pas exactement du système d'unité et de la base de vecteurs choisie:
Si maintenant l'espace n'est pas le même dans toutes les directions, par exemple s'il est courbe comme sur la surface de la Terre, ou si certaines directions sont privilégiées par rapport à d'autres, on doit mesurer les quantités dans toutes les directions.
Sur la terre, par exemple, marcher 1000 km vers l'est, 1000 km vers le Nord, 1000 km vers le Sud, et enfin 1000 km vers Ouest ne nous permet pas de revenir au point initial à cause de la courbure terrestre: D'où l'importance de tenir compte de la direction de la mesure. C'est là que le tenseur est interessant.
C'est similaire dans un cristal où la conductivité serait plus forte suivant certaines directions que d'autres: cela va affecter la manière dont le courant électrique va vouloir circuler: on a alors un tenseur de conductivité plutôt que juste un nombre.
Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
Re: Tenseurs
par tim9.5 Ven 25 Mar 2016 - 3:39
Petite question :est-ce que le tenseur métrique s'utilise avec la formule "intégrale de a à b racine(ds2)" comme proposé dans le wiki tenseur métrique ?
Mais je ne comprend pas pourquoi.
Le ds signifie qu'on a bougé un tout petit peu de place (un peu au nord, un peu à l'est ou un peu selon r, un peu selon l'angle pour les coordonnées polaires).
L'intégrale signifie qu'on rajoute nos petits ds bout à bout et qu'on les additionne.
Mais alors, où est indiqué le chemin "1000 km vers l'est, 1000 ks vers le nord, 1000 km vers le sud" ? Il manque une fonction f(s) qui paramètre le chemin choisi à intégrer, à moins que le tenseur contient déjà la géodésique qui relie 2 points a et b.
Où est le bug ?
Mais je ne comprend pas pourquoi.
Le ds signifie qu'on a bougé un tout petit peu de place (un peu au nord, un peu à l'est ou un peu selon r, un peu selon l'angle pour les coordonnées polaires).
L'intégrale signifie qu'on rajoute nos petits ds bout à bout et qu'on les additionne.
Mais alors, où est indiqué le chemin "1000 km vers l'est, 1000 ks vers le nord, 1000 km vers le sud" ? Il manque une fonction f(s) qui paramètre le chemin choisi à intégrer, à moins que le tenseur contient déjà la géodésique qui relie 2 points a et b.
Où est le bug ?
tim9.5- Messages : 451
Date d'inscription : 18/10/2014
Re: Tenseurs
par Badak Ven 25 Mar 2016 - 6:00
Oui c'est ça. Le ds est un "infinitésimal" qui est égal à racine de ( somme des gij * dx_i * dx_j ) , où gij est le tenseur métrique.tim9.5 a écrit:Petite question :est-ce que le tenseur métrique s'utilise avec la formule "intégrale de a à b racine(ds2)" comme proposé dans le wiki tenseur métrique ?
Mais je ne comprend pas pourquoi.
Le ds signifie qu'on a bougé un tout petit peu de place (un peu au nord, un peu à l'est ou un peu selon r, un peu selon l'angle pour les coordonnées polaires). L'intégrale signifie qu'on rajoute nos petits ds bout à bout et qu'on les additionne.
C'est presque exactement comme lorsque la distance est euclidienne, sauf que dans ce cas-là le tenseur est une matrice diagonale et le produit des dx_i et dx_j devient un produit scalaire ordinaire, et ds est l'hypothénuse du triangle infinitésimal formé des côtés dx_i et dx_j.
Quand la distance est euclidienne, toutes les lignes droites sont des géodésiques, mais attention, lorsque le tenseur métrique est quelconque, on ne sait pas apriori en général la direction dans laquelle se trouve la géodésique... Pour le savoir on doit le déduire d'un calcul variationnel qui consiste à minimiser la distance en chaque point (avec la distance définie par l'intégrale plus-haut. )
Si on dit "marcher vers l'est ", dans le cas de la Terre, par exemple, c'est donner une direction. On pourrait paramétrer ça effectivement (genre avec un angle autour de l'axe de rotation de la Terre).tim9.5 a écrit: Mais alors, où est indiqué le chemin "1000 km vers l'est, 1000 ks vers le nord, 1000 km vers le sud" ? Il manque une fonction f(s) qui paramètre le chemin choisi à intégrer, à moins que le tenseur contient déjà la géodésique qui relie 2 points a et b.
Où est le bug ?
Sauf que justement aller tout "droit" vers l'est, ce n'est pas une géodésique, alors qu'aller "tout droit" vers le sud donne une géodésique. Les géodésiques sont les chemins qui minimisent la distance entre deux points "à vol d'oiseau", et aller vers l'est en suivant un parralèle terrestre fait un cercle qui n'est pas le chemin le plus court...
- les géodésiques:
- Pour s'en rendre compte, il suffit de prendre un bout de ficelle sur un globe terrestre pour relier deux points sur le même parallèle. Les méridiens, eux, sont bel et bien des géodésiques.
On peut aussi jouer à couper une orange suivant différentes directions: couper suivant les "parallèles" fait des tranches tandis que couper suivant les méridiens terrestres produit des "quartiers d'orange":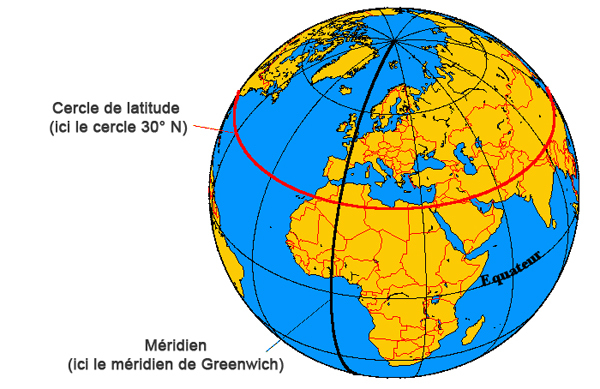
Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
Tenseurs
par tim9.5 Ven 25 Mar 2016 - 20:41
Merci pour ta réponse.
Deux petites notes :
Deux petites notes :
- Erratum géodésique sphérique:
- Les géodésiques sphériques sont des arcs de cercles. Une demi-parallèle et plus petit sont donc des géodésiques. Sinon je devrais passer par le pôle nord pour me rendre d'Italie en France le plus rapidement possible:-)
- Penser comme un physicien:
- Depuis quelques temps, je me suis mis à la physique théorique par les supports écrits et les vidéos (et cette section) en essayant le point de vue du physicien. Et c'est dingue comme on comprend mieux les formules ! Par exemple, quand tu écris ton intégrale en écriture curviligne +
Ca m'a fait un tilt dans ma tête : dériver + intégrer + minimiser, c'est de la technique lagrangienne avec sa cousine germaine hamiltonienne. Ne pourrait-on pas minimiser l'énergie entre deux points ?Pour le savoir on doit le déduire d'un calcul variationnel qui consiste à minimiser la distance en chaque point (avec la distance définie par l'intégrale plus-haut. )
Dans un deuxième temps, ton commentaire sur les géodésiques m'a chicané. J'ai donc cherché "géodésique" sur le wiki. Et voilà le résultat :L'équation géodésique est également l'équation d'Euler-Lagrange associée à l'énergie de la courbe :
E(\gamma) = \int g_{\gamma(\lambda)}(V(\lambda),V(\lambda))d\lambda
Comme le Lagrangien L(\lambda, \gamma, V) = g_\gamma(V,V) est indépendant du temps λ, le Hamiltonien se conserve le long des géodésiques. Or ici le Hamiltonien est égal au Lagrangien, lui-même égal au carré de la norme de la vitesse. On conclut que la vitesse se conserve le long des géodésiques, en accord avec leur absence d'accélération.
Et du même coup, en copiant ce texte je vois comment tu as fait pour écrire ta formule avec de jolis symboles.
La pêche a été bonne aujourd'hui.
tim9.5- Messages : 451
Date d'inscription : 18/10/2014
Re: Tenseurs
par Badak Sam 26 Mar 2016 - 7:07
tim9.5 a écrit:Les géodésiques sphériques sont des arcs de cercles. Une demi-parallèle et plus petit sont donc des géodésiques. Sinon je devrais passer par le pôle nord pour me rendre d'Italie en France le plus rapidement possible:-)
Les géodésiques sont des arcs de cercles, MAIS pas tous les arcs de cercles sont des géodésiques. En particulier comme je disais plus haut, les parallèles de la Terre ne sont pas des géodésiques parce qu'elles ne suivent pas le chemin le plus court. En réalité, il n'y a même qu'à l'équateur qu'un parallèle est en même temps une géodéqique.
Et pour aller de la France au Japon par le plus court chemin (c-a-d par une géodésique), on devrait passer au dessus de l'arctique environ, et non pas suivre un parralèle.
oui, c'est exactement ça. En mécanique, les trajectoires suivies par des particules sont les géodésiques d'un espace dont le tenseur métrique est relié à l'energie.tim9.5 a écrit: Depuis quelques temps, je me suis mis à la physique théorique par les supports écrits et les vidéos (et cette section) en essayant le point de vue du physicien. ....
Ca m'a fait un tilt dans ma tête : dériver + intégrer + minimiser, c'est de la technique lagrangienne avec sa cousine germaine hamiltonienne. Ne pourrait-on pas minimiser l'énergie entre deux points ?
En fait, l'energie cinétique, par exemple, s'écrit comme une somme( E_ij * vi*vj ), où les vi, vj notent les vitesses selon les directions i et j. Et dans ce cas, E_ij est une matrice qu'on peut regarder comme un tenseur métrique.
En mécanique, ce que le principe de moindre action demande de minimiser, c'est l'intégrale d'action. Et on peut la considérer comme une "distance" totale. Dans le cas le plus simple où les particules sont libres et qu'il n'y a pas de potentiel, l'élément infinitésimal de distance ds sera comme dans le post précédent, mais avec E_ij à la place de g_ij pour jouer le rôle de tenseur métrique.
Tu sembles avoir déjà les bases en calcul différentiel et intégral, alors tu as raison, on voit mieux à quoi servent les maths quand on se rend compte des applications à la physique. Et à l'ingénierie aussi, parce que toute l'approche hamiltonienne se généralise ensuite pour donner lieu à la théorie du contrôle optimal qui est utilisée par exemple par les ingénieurs qui doivent planifier des trajectoires qui minimise une certaine fonction de "coût".
Pour continuer avec la physique et les tenseurs, disons que ce qui est interessant est que ce tenseur métrique est lié "d'une certaine façon" à la courbure de la surface et à la topologie de la surface sur laquelle on est. Et tout ça concerne d'autres tenseurs.
Ce qu'on fait ici sur la surface 2D de la Terre, avec le tenseur métrique et la courbure, c'est à peu près la même chose ensuite en 4D lorsqu'on regarde l'espace-temps de la relativité générale: la différence est surtout que ce ne se passe plus sur une sphère.
Ouais j'ai juste emprunté l'image à wiki, parce que sinon c'est long à réécrire.tim9.5 a écrit: Et du même coup, en copiant ce texte je vois comment tu as fait pour écrire ta formule avec de jolis symboles.
Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
Re: Tenseurs
par tim9.5 Mer 30 Mar 2016 - 17:26
Merci pour tes explications. J'ai une meilleure intuition là-dessus.
En revanche, je ne cerne pas bien la notion de tenseur de containtes.
Je ne comprends pas comment passer de 6 forces à un tenseur (3x3), et comment visualiser celui-ci.
Peut-on avoir un petit exemple à partir d'un cube déformé de plusieurs manières ?
En revanche, je ne cerne pas bien la notion de tenseur de containtes.
Hobb a écrit:Tu prends un cube, et sur chaque face tu exerces une force. Sur chaque face du cube, tu as une force différente. Une force c'est un vecteur, donc sur chazque direction X,Y,Z du cube, tu auras une force qui a 3 composantes. Pour symboliser cette contrainte, on utilise un tenseur 3x3, qui pour chaque direction du cube te donne le vecteur force qui est exercé. Voilà, c'est tout. C'est le tenseur des contraintes qui est un tenseur 3x3.
Je ne comprends pas comment passer de 6 forces à un tenseur (3x3), et comment visualiser celui-ci.
Peut-on avoir un petit exemple à partir d'un cube déformé de plusieurs manières ?
- Spoiler:
ou 
et 
tim9.5- Messages : 451
Date d'inscription : 18/10/2014
Re: Tenseurs
par Invité Mer 30 Mar 2016 - 17:40
Il faut aller dans le sujet "tenseurs" d'origine Je n'y connais rien. J'ouvrirai un fil "tenseurs pour les nuls pour devenir moins nuls 
" pour ceux celles qui souhaitent s'y intéresser
ou attendre que soit remis l'auteur pro du tenseur de ce fil en auteur ainsi qu'on enlève tous mes messages ici
Je n'y connais rien. J'ouvrirai un fil "tenseurs pour les nuls pour devenir moins nuls " pour ceux celles qui souhaitent s'y intéresser ou attendre que soit remis l'auteur pro du tenseur de ce fil en auteur
ainsi qu'on enlève tous mes messages ici
Invité- Invité
Re: Tenseurs
par prométhéus Jeu 31 Mar 2016 - 22:51
Natatypique a écrit:Il faut aller dans le sujet "tenseurs" d'origine
ou attendre que soit remis l'auteur pro du tenseur de ce fil en auteur
L'étape d'après l'autocollant "I LOVE TENSOR" à coller sur la voiture
, on appelle çà la technique du pied dans la porte , parait-il Après cela sera les séminaires ...
prométhéus- Messages : 361
Date d'inscription : 26/04/2015
Age : 43
Localisation : troisième planète du système solaire
Re: Tenseurs
par Invité Jeu 31 Mar 2016 - 23:42
prométhéus a écrit:Natatypique a écrit:Il faut aller dans le sujet "tenseurs" d'origine
ou attendre que soit remis l'auteur pro du tenseur de ce fil en auteur
L'étape d'après l'autocollant "I LOVE TENSOR" à coller sur la voiture
Après cela sera les séminaires ...
A chaque fois qu'il y a distribution d'un truc sympa, je ne suis pas là (m'en fous j'ai pas de voiture, et si je le colle sur mon front... je vais encore avoir à gérer un relationnel "tendu" et ça va finir en "et ta soeur"....)
(m'en fous j'ai pas de voiture, et si je le colle sur mon front... je vais encore avoir à gérer un relationnel "tendu" et ça va finir en "et ta soeur"....)Plus sérieusement je dois avoir un syndrome du "savoir où il se trouve le savoir" mais marre qu'il ne se diffuse pas ? ça n'est pas normal qu'il passe par moi, celui qui ne sait pas,
je ne sais rien !!!....
Je vais faire des recherches dans le fil des "transmetteurs", ils doivent faire de la rétention, ça arrive quand on fait trop de voiture....
Ca tombe je suis en train de monter un complot à l'insu de mon plein gré, pour que tout le monde dépose son savoir ici et pouvoir qui sait y envoyer tout le monde...
On ne sait pas ce qui peut se passer dans ces cerveaux ? la maîtrise des connexions tout ça, même pas un petit mode d'emploi en magnet à mettre sur le frigo pour s'en souvenir ou un système régulateur comme dans les ascenseurs ?
"vous êtes en surcharge de connaissances, veuillez prendre immédiatement l'escalier de l'ignorance".
Y'a qu'ici qu'on peut faire de la surcharge cognitive rien qu'à l'idée de ce à quoi on va pourvoir s'intéresser.
C'est le "syndrome de la surcharge cognitive d'anticipation du savoir", il faut le savoir, ça comprend des risques, comme le "syndrome de l'apprentissage". Donc je me fais mes dégradés : "mode apprenti sage" "mode ingestion", "mode assimilation", "mode digestion", c'est expliqué nulle part tout ça même pas un petit livre, un petit code de la route : vous venez d'entrer inopinément dans la zone "grosses connaissances", alerte, risque de saturation, veuillez vous diriger immédiatement vers le sas de décompression...
Donc je me fais mes dégradés : "mode apprenti sage" "mode ingestion", "mode assimilation", "mode digestion", c'est expliqué nulle part tout ça même pas un petit livre, un petit code de la route : vous venez d'entrer inopinément dans la zone "grosses connaissances", alerte, risque de saturation, veuillez vous diriger immédiatement vers le sas de décompression...Ca doit être pour ça que j'avais vu un lien entre douance et ce fil "tenseurs" (une trouvaille pour baisser la tension ?, ben non tout plein d'équations).
C'est tout à fait cela, personne n'a encore découvert le "syndrome de l'autocollant", pourtant c'est évident...
(j'adore l'image de l'autocollant).
Merci, je garde.
Mieux vaut "séminer" que "se miner" 
Je garde aussi, entre autres,
Ainsi que "le pied dans la porte", au moins c'est déjà une très grande avancée scientifique sur le "cul entre deux chaises". Si ça continue, on va même pouvoir s'asseoir..... un jour.
ps : le film ? c'était vous ?
Merci pour l'entrée en matière, j'ai bien ri (ni l'endroit ni la place, mais bon...
"Il faut savoir se détendre" !!!! 
De toute façon, je suppose qu'aucune étude n'est en cours sur "la théorie de la tringle à rideaux qui tient le rideau derrière lequel j'aurai aimé aller me cacher en mode disparation immédiate quand j'ai vu mon pseudo associé aux "tenseurs".
Il y a aussi un "syndrome de la mémoire sélective", et celui de "l'association d'idées", je préfère désormais plutôt être associé à "2 de tension" dans la majorité des esprits. (ça c'est la faute à un doué fan de cardio... 
) et pouvoir dire :
) et pouvoir dire : "taka aller voir ZB, il sait tout" .
. Sinon, au cas où, vous savez si ils font des autocollants au fait "ZB" ?
On nous cache tout, on nous dit rien. Complot.
Invité- Invité
Re: Tenseurs
par Badak Jeu 31 Mar 2016 - 23:54
Natatypique a écrit:Il faut aller dans le sujet "tenseurs" d'origine
ou attendre que soit remis l'auteur pro du tenseur de ce fil en auteur
Tu as raison, Natalie (ou natashquan ? ), le sujet est périlleux: L'important est d'indiquer dans quelle direction le fil est tendu.
Mais quand c'est un fil, c'est encore trop simple, quand il y 3 directions qui se déforment, c'est bien plus grave et risqué:
Les contraintes et les déformations ne sont pas les mêmes suivant toutes les directions : il y par exemple traction/compression mais aussi le cisaillement.
Si on représente la relation entre les deux par une relation linéaire, c'est la loi de Hooke
Ça c'est dans le cas de l'élasticité.
La bête qui fait le lien entre la contrainte et la déformation s'appelle un tenseur. On peut le voir comme une matrice, mais en plus général.
Ce serait exactement la même chose avec le tenseur de conductivité en électricité qui exprime la relation entre le courant et le champs électrique.
Le reste c'est des détails mathématiques pour noter tout cela, mais le tenseur lui-même est un objet mathématique, donc on peut communiquer l'idée de la physique derrière avec des schémas, mais c'est difficile d'expliquer davantage sans écrire d'équation.
Natatypique a écrit:"syndrome de la surcharge cognitive d'anticipation du savoir"
Ah oui d'accord
OMG. C'est exactement mon problème. Parfois il y a des choses que j'aimerais savoir et quand je vais voir les sources censées pouvoir me l'expliquer.... Je suis pris d'un vertige (comme un funambule) au dessus de l'abime de mon ignorance... Je sais un peu de tout mais tellement superficiellement que je n'arrive pas à travailler du fait qu'il me semble que je dois apprendre à creuser. Mais plus je creuse et plus l'abime de l'ignorance s'agrandit. Les livres de maths (les vrais, pas ceux des physicens) sont fabuleux pour les funambules: ils sont impénétrables de la beauté vertigineuse d'un savoir supposément accessible mais qui se dérobe pour qui n'a pas pris le temps de se taper les 200 pages précédent le seul foutu passage vraiment utile.. Cela créé effectivement une tension interieure semblable à celle de la poésie, comme la sensation de se retrouver devant un texte en chinois pour la première fois en se disant que cela a un sens et qu'il me suffit simplement de l'étudier pour y accéder.
Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
Re: Tenseurs
par prométhéus Sam 2 Avr 2016 - 22:37
Natatypique a écrit:prométhéus a écrit:Natatypique a écrit:Il faut aller dans le sujet "tenseurs" d'origine
ou attendre que soit remis l'auteur pro du tenseur de ce fil en auteur
L'étape d'après l'autocollant "I LOVE TENSOR" à coller sur la voiture
Après cela sera les séminaires ...A chaque fois qu'il y a distribution d'un truc sympa, je ne suis pas làPlus sérieusement je dois avoir un syndrome du "savoir où il se trouve le savoir" mais marre qu'il ne se diffuse pas ? ça n'est pas normal qu'il passe par moi, celui qui ne sait pas,je ne sais rien !!!....Je vais faire des recherches dans le fil des "transmetteurs", ils doivent faire de la rétention, ça arrive quand on fait trop de voiture....Ca tombe je suis en train de monter un complot à l'insu de mon plein gré, pour que tout le monde dépose son savoir ici et pouvoir qui sait y envoyer tout le monde...On ne sait pas ce qui peut se passer dans ces cerveaux ? la maîtrise des connexions tout ça, même pas un petit mode d'emploi en magnet à mettre sur le frigo pour s'en souvenir ou un système régulateur comme dans les ascenseurs ?"vous êtes en surcharge de connaissances, veuillez prendre immédiatement l'escalier de l'ignorance".Y'a qu'ici qu'on peut faire de la surcharge cognitive rien qu'à l'idée de ce à quoi on va pourvoir s'intéresser.C'est le "syndrome de la surcharge cognitive d'anticipation du savoir", il faut le savoir, ça comprend des risques, comme le "syndrome de l'apprentissage".Ca doit être pour ça que j'avais vu un lien entre douance et ce fil "tenseurs" (une trouvaille pour baisser la tension ?, ben non tout plein d'équations).C'est tout à fait cela, personne n'a encore découvert le "syndrome de l'autocollant", pourtant c'est évident...(j'adore l'image de l'autocollant).Merci, je garde.Mieux vaut "séminer" que "se miner"Je garde aussi, entre autres,Ainsi que "le pied dans la porte", au moins c'est déjà une très grande avancée scientifique sur le "cul entre deux chaises". Si ça continue, on va même pouvoir s'asseoir..... un jour.ps : le film ? c'était vous ?Merci pour l'entrée en matière, j'ai bien ri (ni l'endroit ni la place, mais bon..."Il faut savoir se détendre" !!!!De toute façon, je suppose qu'aucune étude n'est en cours sur "la théorie de la tringle à rideaux qui tient le rideau derrière lequel j'aurai aimé aller me cacher en mode disparation immédiate quand j'ai vu mon pseudo associé aux "tenseurs".Il y a aussi un "syndrome de la mémoire sélective", et celui de "l'association d'idées", je préfère désormais plutôt être associé à "2 de tension" dans la majorité des esprits. (ça c'est la faute à un doué fan de cardio..."taka aller voir ZB, il sait tout"Sinon, au cas où, vous savez si ils font des autocollants au fait "ZB" ?On nous cache tout, on nous dit rien. Complot.
Nous avons des magnets, par contre nous ne fournissons ni les cottes de mailles ni les portes de frigos, qui on le sait sont les écosystèmes de prédilection des magnets sauvages ou d'élevages.
prométhéus- Messages : 361
Date d'inscription : 26/04/2015
Age : 43
Localisation : troisième planète du système solaire
Re: Tenseurs
par tim9.5 Dim 3 Avr 2016 - 22:54
Tenseur métrique pour les nuls, vu par un amateur :
Tu décides d'aller d'un point à un autre (lors d'une promenade ou un grand voyage). Et à chaque fois, ton petit cousin pénible demande : "'c'est encore loin?".
Afin d'arrêter d'être cisaillé du cerveau par cette question sans réponse, tu décides d'inventer un truc qui l'occupe durant votre prochaine expédition : un odomètre (rien à voir avec les cellules olfactives).
Plusieurs versions possibles :
a) la version rurale da Vinci :
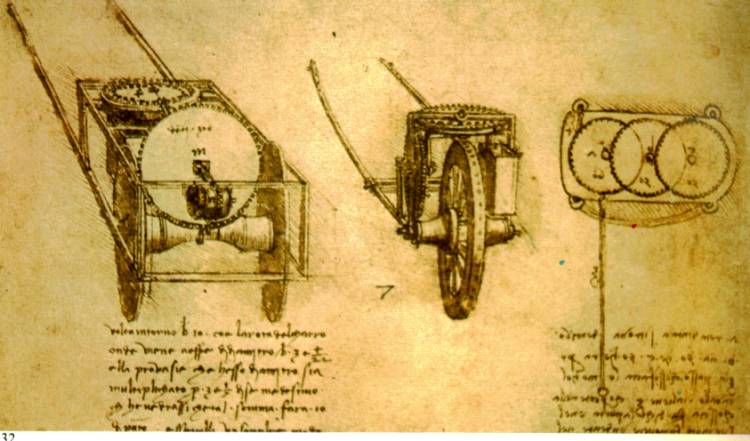
b) la version du riche chinois, très festive : (en fait je ne vois pas le lien mais il y en a un selon wik. Peut-être que, buvant régulièrement, les personnages tombent chaque kilomètre exactement. Poucet Junior aurait adapté cette idée à son âge avec les moyens du bord.)
c) la version du geek : un podomètre.
d) la version du bushman : le curvimètre + une carte de géo.
http://bushcraftdalex.blogspot.de/2014/04/le-curvimetre.html
d) la version du mathématicien qui aime porter des trucs légers sans vraiment les constuire :
C'est la jolie formule du début de ce fil, écrite par Badak (et que je n'arrive pas à reproduire, en fait) avec des gij. (Mais pas de "ciji mon intelligence"!)
Les gij sont des bouts de tenseurs métriques, ou si tu préfères un morceau de chocolat spécial dans une boîte carrée :
Si tu veux prendre celui certi d'une demi-noix, tu le trouves à la g32 ème place (3 et 2 écrits en petit). Compris ? La boîte de choc s'appelle une maTrix !
Mais qui a inventé le premier tenseur métrique ?
De source à peu près sûre, Giorgio Ricci-Curbastro(physicien relatif généraliste, quelle coincidence !) se promenait vers 1920 avec son cousin muni d'une version high-tech de l'odomètre de Leonard di Vinci, sur un glacier italien.
Hélas, ledit enfant tomba soudainement dans une crevasse. Ayant constaté qu'il n'avait rien de grave, Giogio lui cria : "as-tu pu au moins mesurer la longueur de ta chute ?"
- Non, car je n'ai pas pu faire tourner la roue contre la paroi ! En revanche, j'ai trouvé des magnets sauvages d'origine préhumaine (et oui, le garnement était déjà abonné à l'encyclopédie universalis) et congelé dans la glace.
Cela fit d'une pierre deux coups :
a) Giorgio, tancé vertement par la maman de l'égratigné, préféra parcourir des distances sur papier, et devint l'inventeur du Tenseur de Ricci qui permet de mesurer correctement des longueurs dans l'espace-temps pas trop tiraillé. Einstein en profita pour l'injecter dans son équation sur la relativité générale.
b) Pour suivre le mouvement initié par sa maman et Giorgio, le cousin lança le premier club de soutien des tenseurs avec qui j'ai la joie de correspondre dans ce fil.
La simulation d'une chute dans une crevasse fut tensorisée plus tard. On trouva même les chemins le plus court (les géodésiques) pour ne pas se casser la gueule à grande vitesse près d'un soleil : (en rouge ici. L'espace (et le temps) est déformé par un soleil au fond de la poche).
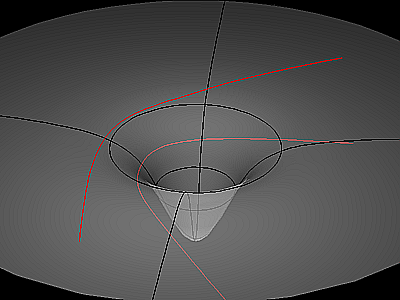
Tape "relativité générale" dans le wiki pour plus de détails.
Conclusion : pour comprendre la relativité générale, regarde d'abord les animations et les équations finales qui fricotent avec moults tenseurs, mais n'essaye pas de trop les gratter, car un gouffre mathématique s'ouvrira devant toi ! (Les maTrix étant plus ludiques et aisées à manipuler).
Tu décides d'aller d'un point à un autre (lors d'une promenade ou un grand voyage). Et à chaque fois, ton petit cousin pénible demande : "'c'est encore loin?".
Afin d'arrêter d'être cisaillé du cerveau par cette question sans réponse, tu décides d'inventer un truc qui l'occupe durant votre prochaine expédition : un odomètre (rien à voir avec les cellules olfactives).
Plusieurs versions possibles :
a) la version rurale da Vinci :
b) la version du riche chinois, très festive : (en fait je ne vois pas le lien mais il y en a un selon wik. Peut-être que, buvant régulièrement, les personnages tombent chaque kilomètre exactement. Poucet Junior aurait adapté cette idée à son âge avec les moyens du bord.)
c) la version du geek : un podomètre.
d) la version du bushman : le curvimètre + une carte de géo.
http://bushcraftdalex.blogspot.de/2014/04/le-curvimetre.html
d) la version du mathématicien qui aime porter des trucs légers sans vraiment les constuire :
C'est la jolie formule du début de ce fil, écrite par Badak (et que je n'arrive pas à reproduire, en fait) avec des gij. (Mais pas de "ciji mon intelligence"!)
Les gij sont des bouts de tenseurs métriques, ou si tu préfères un morceau de chocolat spécial dans une boîte carrée :
Si tu veux prendre celui certi d'une demi-noix, tu le trouves à la g32 ème place (3 et 2 écrits en petit). Compris ? La boîte de choc s'appelle une maTrix !
- explication:
- Le premier chiffre (ici trois) correspond à la 3ème ligne de la boîte. Le deuxième chiffre, à la 2ème colonne de la boîte. Ainsi g56 = choc 5ème ligne, 6ème colonne.
Mais qui a inventé le premier tenseur métrique ?
De source à peu près sûre, Giorgio Ricci-Curbastro(physicien relatif généraliste, quelle coincidence !) se promenait vers 1920 avec son cousin muni d'une version high-tech de l'odomètre de Leonard di Vinci, sur un glacier italien.
Hélas, ledit enfant tomba soudainement dans une crevasse. Ayant constaté qu'il n'avait rien de grave, Giogio lui cria : "as-tu pu au moins mesurer la longueur de ta chute ?"
- Non, car je n'ai pas pu faire tourner la roue contre la paroi ! En revanche, j'ai trouvé des magnets sauvages d'origine préhumaine (et oui, le garnement était déjà abonné à l'encyclopédie universalis) et congelé dans la glace.
Cela fit d'une pierre deux coups :
a) Giorgio, tancé vertement par la maman de l'égratigné, préféra parcourir des distances sur papier, et devint l'inventeur du Tenseur de Ricci qui permet de mesurer correctement des longueurs dans l'espace-temps pas trop tiraillé. Einstein en profita pour l'injecter dans son équation sur la relativité générale.
b) Pour suivre le mouvement initié par sa maman et Giorgio, le cousin lança le premier club de soutien des tenseurs avec qui j'ai la joie de correspondre dans ce fil.
La simulation d'une chute dans une crevasse fut tensorisée plus tard. On trouva même les chemins le plus court (les géodésiques) pour ne pas se casser la gueule à grande vitesse près d'un soleil : (en rouge ici. L'espace (et le temps) est déformé par un soleil au fond de la poche).
Tape "relativité générale" dans le wiki pour plus de détails.
Conclusion : pour comprendre la relativité générale, regarde d'abord les animations et les équations finales qui fricotent avec moults tenseurs, mais n'essaye pas de trop les gratter, car un gouffre mathématique s'ouvrira devant toi ! (Les maTrix étant plus ludiques et aisées à manipuler).
tim9.5- Messages : 451
Date d'inscription : 18/10/2014
Re: Tenseurs
par tim9.5 Mar 5 Avr 2016 - 20:47
Coucou, Natatypique ! T'es toujours derrière ton rideau avec tout plein de visiteurs qui n'osent poster quelque chose de peur d'être pris pour un imbécile ;-)
Saches que j'ai tellement ri de tes messages que ça m'a inspiré le pavé ci-dessus dans un style youplàboum pour dédramatiser les tenseurs et tous les constructions physico-mathématiques. Hi, hi, hi.
Saches que j'ai tellement ri de tes messages que ça m'a inspiré le pavé ci-dessus dans un style youplàboum pour dédramatiser les tenseurs et tous les constructions physico-mathématiques. Hi, hi, hi.
tim9.5- Messages : 451
Date d'inscription : 18/10/2014
Re: Tenseurs
par prométhéus Dim 22 Mai 2016 - 0:32
tim9.5 a écrit:Coucou, Natatypique ! T'es toujours derrière ton rideau avec tout plein de visiteurs qui n'osent poster quelque chose de peur d'être pris pour un imbécile ;-)
Saches que j'ai tellement ri de tes messages que ça m'a inspiré le pavé ci-dessus dans un style youplàboum pour dédramatiser les tenseurs et tous les constructions physico-mathématiques. Hi, hi, hi.
Je crois que le problème est qu'un concept a besoin d'être collé à une certaine utilité,or si la notion de vecteur est bien visible dans la vie de tous les jours, le tenseur se montre quand à lui plus timide.
prométhéus- Messages : 361
Date d'inscription : 26/04/2015
Age : 43
Localisation : troisième planète du système solaire
Re: Tenseurs
par Badak Dim 22 Mai 2016 - 19:54
prométhéus a écrit:tim9.5 a écrit:Coucou, Natatypique ! T'es toujours derrière ton rideau avec tout plein de visiteurs qui n'osent poster quelque chose de peur d'être pris pour un imbécile ;-)
Saches que j'ai tellement ri de tes messages que ça m'a inspiré le pavé ci-dessus dans un style youplàboum pour dédramatiser les tenseurs et tous les constructions physico-mathématiques. Hi, hi, hi.
Je crois que le problème est qu'un concept a besoin d'être collé à une certaine utilité,or si la notion de vecteur est bien visible dans la vie de tous les jours, le tenseur se montre quand à lui plus timide.
Je ne pense pas que ce puisse être le problème: les tenseurs sont utilisés partout . Ne serait-ce que partout où il y a de l'élasticité, des fluides, ou des phénomènes anisotropes en général...
Je dirais que c'est que le vecteur, un enfant peut comprendre tout de suite en se le représentant comme une flêche, mais pour les tenseurs, malgré leur présence, il faut au minimum se figurer un changement de coordonnées en plusieurs dimensions.
Le 2D: je crois que tout le monde le voit.
En 3D: c'est plus difficile.
Et le 4D: là déjà les gens demandent "mais c quoi cte 4e dimension ?" Là c'est seulement apprivoiser l'abstraction le problème.
Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
Re: Tenseurs
par prométhéus Mar 24 Mai 2016 - 0:07
Badak a écrit:Je ne pense pas que ce puisse être le problème: les tenseurs sont utilisés partout . Ne serait-ce que partout où il y a de l'élasticité, des fluides, ou des phénomènes anisotropes en général...
Je crois que le problème est qu'un concept a besoin d'être collé à une certaine utilité,or si la notion de vecteur est bien visible dans la vie de tous les jours, le tenseur se montre quand à lui plus timide.
La notion de vecteur va passer comme naturel car il va consister juste à remplacer vecteur par flèche, une accroche qui amènera à une notion plus générale que celle très naturelle de vecteur dans l'espace affine.
De même la notion de matrice pourrait s'approcher via des jeux genre bataille naval, accroche aussi, mais la notion de tenseur, qui est une notion nécessaire pour le physicien notamment pour tout ce qui est méca flu, élasticité, optique en milieu anisotrope, acoustique aussi en relativité , pour Mme Jeufépadefisic cette notion parait totalement inutile , même si elle pourrait servir à décrire beaucoup de choses dans la vie ordinaire de cette dame, bon on pourrait en dire tout autant d'autres notions, qui sont partout en physique comme les sections de fibrés.
Les mathématiques sont absolument partout mais de nature souvent assez timide.
Et ne me répond pas que tu n'es pas d'accord que contrairement à ce que je dis les mathématiques sont partout !
( Le manque de sommeil est mauvais pour la santé
)Dernière édition par prométhéus le Mer 20 Juil 2016 - 23:57, édité 1 fois
prométhéus- Messages : 361
Date d'inscription : 26/04/2015
Age : 43
Localisation : troisième planète du système solaire
Re: Tenseurs
par Badak Mar 24 Mai 2016 - 4:33
oui je m'inclineprométhéus a écrit:Badak a écrit:Je ne pense pas que ce puisse être le problème: les tenseurs sont utilisés partout . Ne serait-ce que partout où il y a de l'élasticité, des fluides, ou des phénomènes anisotropes en général...
Je crois que le problème est qu'un concept a besoin d'être collé à une certaine utilité,or si la notion de vecteur est bien visible dans la vie de tous les jours, le tenseur se montre quand à lui plus timide.
La notion de vecteur va passé comme naturel car il va consister juste à remplacer vecteur par flèche, une accroche qui amènera à une notion plus générale que celle très naturelle de vecteur dans l'espace affine.
De même la notion de matrice pourrait s'approcher via des jeux genre bataille naval, accroche aussi, mais la notion de tenseur, qui est une notion nécessaire pour le physicien notamment pour tout ce qui mécanique flu, élasticité, optique en milieu anisotrope, acoustique aussi en relativité , pour Mme Jeufépadefisic cette notion parait totalement inutile , même si elle pourrait servir à décrire beaucoup de choses dans la vie ordinaire de cette dame, bon on pourrait en dire tout autant d'autres notions, qui sont partout en physique comme les sections de fibrés.
Les mathématiques sont absolument partout mais de nature souvent assez timide.
Et ne me répond pas que tu n'es pas d'accord que contrairement à ce que je dis les mathématiques sont partout !
( Le manque de sommeil est mauvais pour la santé
Bah oui on dit la même chose. En grosÉvidemment je dois ajouter compulsivement un commentaire:
D'une part, je connais des gens qui ne comprennent pas l'idée des vecteurs et encore moins celle des matrices... Avec les matrices, l'idée qui est compliquée, c'est de saisir le pourquoi du produit matriciel... et sa non-commutativité est particulièrement difficile à accepter apparemment. Ce que je veut dire, c'est seulement qu'une fois qu'on comprend les matrices, manipuler les tenseurs est juste une question d'être à l'aise avec la pensée abstraite. Bref, tu ne diras pas réellement le contraire non plus, c'est un peu ridicule d'en débattre en effet
Mais tant qu'à enculer les mouches, aussi bien y aller à fond. et c'est encore mieux à deux
Badak- Messages : 1230
Date d'inscription : 02/12/2011
Localisation : Montréal
Re: Tenseurs
par prométhéus Mar 24 Mai 2016 - 22:22
Badak a écrit:oui je m'inclineprométhéus a écrit:Badak a écrit:Je ne pense pas que ce puisse être le problème: les tenseurs sont utilisés partout . Ne serait-ce que partout où il y a de l'élasticité, des fluides, ou des phénomènes anisotropes en général...
Je crois que le problème est qu'un concept a besoin d'être collé à une certaine utilité,or si la notion de vecteur est bien visible dans la vie de tous les jours, le tenseur se montre quand à lui plus timide.
La notion de vecteur va passé comme naturel car il va consister juste à remplacer vecteur par flèche, une accroche qui amènera à une notion plus générale que celle très naturelle de vecteur dans l'espace affine.
De même la notion de matrice pourrait s'approcher via des jeux genre bataille naval, accroche aussi, mais la notion de tenseur, qui est une notion nécessaire pour le physicien notamment pour tout ce qui mécanique flu, élasticité, optique en milieu anisotrope, acoustique aussi en relativité , pour Mme Jeufépadefisic cette notion parait totalement inutile , même si elle pourrait servir à décrire beaucoup de choses dans la vie ordinaire de cette dame, bon on pourrait en dire tout autant d'autres notions, qui sont partout en physique comme les sections de fibrés.
Les mathématiques sont absolument partout mais de nature souvent assez timide.
Et ne me répond pas que tu n'es pas d'accord que contrairement à ce que je dis les mathématiques sont partout !
( Le manque de sommeil est mauvais pour la santé
Évidemment je dois ajouter compulsivement un commentaire:
D'une part, je connais des gens qui ne comprennent pas l'idée des vecteurs et encore moins celle des matrices... Avec les matrices, l'idée qui est compliquée, c'est de saisir le pourquoi du produit matriciel... et sa non-commutativité est particulièrement difficile à accepter apparemment. Ce que je veut dire, c'est seulement qu'une fois qu'on comprend les matrices, manipuler les tenseurs est juste une question d'être à l'aise avec la pensée abstraite. Bref, tu ne diras pas réellement le contraire non plus, c'est un peu ridicule d'en débattre en effet
Je tiens quand même à préciser que toutes les mouches étaient consentantes .
prométhéus- Messages : 361
Date d'inscription : 26/04/2015
Age : 43
Localisation : troisième planète du système solaire
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum